les Bases en mathématiques : crée

Bonjour,
J'ai des difficultés à comprendre un point sur les bases.
consigne de l'exercice :
Pour trouver l’écriture d’un nombre dans la base seize, on utilise les signes 0-1-2-3-4-5-6-7-8-9-A
pour dix-B pour onze – C pour douze- D pour treize- E pour quatorze- F pour quinze- Trouver l’écriture chiffrée en base seize du nombre
(4^3-1)x(4^3+1)

réponse --> 4^6-1 = (4^2)^3 -1
= 16^3-1

mais je ne parviens pas à comprendre comment passer de la base 3 à la base 16 et trouver le prédécesseur. (ce qu'il y a sur la capture d'écran)
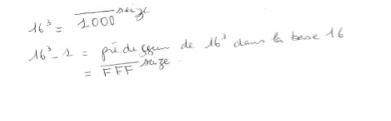
Capture d’écran 2020-12-19 à 18.41.41.png

En vous remerciant par avance ^^

Bonjour,

On ne passe pas de la base 3 à la base 16

On fait ceci :
16³ décimal = 16^3 * 1 + 16² * 0 + 16^1 * 0 + 16^0 * 0

Donc 16³ décimal s'écrit en hexa : 1000

Et en retranchant 1 --> 16³ - 1 en décimal s'écrit en hexa FFF

Bonjour,

@mathcrpe , un complément si besoin ,

$163−1‾(base10)=1000‾(base16)−1‾(base16)\overline{16^3-1}(base 10)=\overline{1000}(base 16)-\overline{1}(base 16)$

Si tu fais la soustraction , avec la disposition usuelle (avec les retenues habituelles), tu trouves :
$1000‾(base16)−1‾(base16)=FFF‾(base16)\overline{1000}(base 16)-\overline{1}(base 16)=\overline {FFF}(base 16)$

Si ce calcul te pose problème, tu peux regarder la vidéo ici (regarde en particulier le second exemple) :
https://www.youtube.com/watch?v=ktL9JF3V6eY

Pour vérifier, tu peux faire la démarche inverse , et mettre $FFF‾(base16)\overline{FFF}(base 16)$ en $b a s e 10$ :
$FFF‾(base16)=162F+16F+F‾(base10)\overline{FFF}(base 16)=\overline{16^2F+16F+F}(base 10)$
$FFF‾(base16)=(162×15)+(16×15)+15‾(base10)\overline{FFF}(base 16)=\overline{(16^2\times 15)+(16\times 15)+15 }(base 10)$
$FFF‾(base16)=4095‾(base10)\overline{FFF}(base 16)=\overline{4095}(base 10)$
$FFF‾(base16)=4096−1‾(base10)\overline{FFF}(base 16)=\overline{4096-1}(base 10)$
$FFF‾(base16)=163−1‾(base10)\overline{FFF}(base 16)=\overline{16^3-1}(base 10)$

Bons calculs !