Montrer qu'une fonction est polynomiale et de degré 2
-
MMOUNA8 dernière édition par
Bonjour, j'ai du mal à résoudre la question c.
Soient X et Y deux vecteurs de même dimension.
a) Montrer que X.X=llXll^2
b) En déduire que llX+Yll^2=llXll^2+2X.Y+llYll^2
c) On considère l’application f : λ ∈ R 7→llX+λYll^2
Montrer que f est une fonction polynomiale de
degré 2 positive ou nulle. Que peut-on en déduire quant au discriminant associé à f ?
d) En déduire l’inégalité de Cauchy-Schwarz
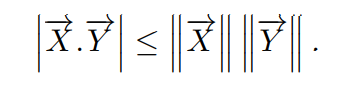
-
mtschoon dernière édition par mtschoon

@mimims , bonjour,
Tu ne donnes guère d'indications sur ce que tu as fait...
Je regarde un peu.
a) Utilise la définition de norme que ton cours de donne.
En principe,
∣∣X→∣∣||\overrightarrow{X}||∣∣X∣∣=X→.X→\sqrt{\overrightarrow{X}.\overrightarrow{X}}X.X
Tu élèves au carré pour obtenir la relation proposée.
Cette question est là pour d'indiquer la méthode à utiliser pour les questions suivantes.b) Tu utilises la propriété du a) au vecteur X→+Y→\overrightarrow{X}+\overrightarrow{Y}X+Y
Ainsi :
∣∣X→+Y→∣∣2=(X→+Y→).(X→+Y→)||\overrightarrow{X}+\overrightarrow{Y}||^2=(\overrightarrow{X}+\overrightarrow{Y}).(\overrightarrow{X}+\overrightarrow{Y})∣∣X+Y∣∣2=(X+Y).(X+Y)Tu développes le membre de droite, tu mets les normes au bons endroits et tu obtiens la relation demandée
c) Tu as dû faire une faute de frappe car le 7 que tu mets n'a aucun sens... je pense qu'il s'agit de λ\lambdaλ
Toujours la même méthode ( vu au a) et au b) )
f(λ)=∣∣X→+λY→∣∣2=(X→+λY→).(X→+λY→)f(\lambda)=||\overrightarrow{X}+\lambda \overrightarrow{Y}||^2=(\overrightarrow{X}+\lambda\overrightarrow{Y}).(\overrightarrow{X}+\lambda\overrightarrow{Y})f(λ)=∣∣X+λY∣∣2=(X+λY).(X+λY)
Tu fais comme pour la b) : tu développes le membre de droite, tu mets les normes aux bons endroits et tu trouves (en l'ordonnant suivant les puissances décroissantes de λ\lambdaλ:
f(λ)=∣∣Y→∣∣2λ2+2λX→.Y→+∣∣X→∣∣2f(\lambda)=||\overrightarrow{Y}||^2\lambda ^2+2\lambda \overrightarrow{X}.\overrightarrow{Y}+||\overrightarrow{X}||^2f(λ)=∣∣Y∣∣2λ2+2λX.Y+∣∣X∣∣2
f(λ)f(\lambda)f(λ) est le carré d'une norme , donc f(λ)≥0\boxed{f(\lambda)\ge 0}f(λ)≥0Tu fais à part le cas particulier ∣∣Y∣∣2=0||Y||^2=0∣∣Y∣∣2=0 et tu obtiens le cas d'égalité de Cauchy-Schwarz
Pour ∣∣Y∣∣2≠0||Y||^2\ne 0∣∣Y∣∣2=0, f(λ)f(\lambda)f(λ) est polynôme du second degré ayant un signe constant, donc son discriminant est négatif : Δ≤0\Delta\le 0Δ≤0
d) Tu explicites Δ\DeltaΔ et tu le divises par 4, d'où, après transposition :
(X→.Y→)2≤∣∣X→∣∣2×∣∣Y→2∣∣(\overrightarrow{X}.\overrightarrow{Y})^2\le ||\overrightarrow{X}||^2\times ||\overrightarrow{Y}^2||(X.Y)2≤∣∣X∣∣2×∣∣Y2∣∣
En prenant la racine carrée de chaque membre, tu obtiens l'inégalité de Cauchy-Schwarz
∣X→.Y→∣≤∣∣X→∣∣×∣∣Y→∣\boxed{|\overrightarrow{X}.\overrightarrow{Y}|\le ||\overrightarrow{X}||\times ||\overrightarrow{Y}|}∣X.Y∣≤∣∣X∣∣×∣∣Y∣
Je t'ai donné la trame du travail mais il faut développer tous les calculs.
Bons calculs .
-
MMOUNA8 dernière édition par
Bonjour, je vous remercie pour votre réponse mais je n'arrive vraiment pas à comprendre pourquoi f(lambda) est supérieur ou égale à 0
-
mtschoon dernière édition par

@mimims ,
Réponse à ta dernière question :
Parce que f(λ)f(\lambda)f(λ) est une norme (et au carré en plus !)
ton énoncé indique :
f(λ)=∣∣X→+Y→∣∣2f(\lambda)=||\overrightarrow{X}+\overrightarrow{Y}||^2f(λ)=∣∣X+Y∣∣2, d'où son signe.
-
MMOUNA8 dernière édition par
@mtschoon je vous remercie, tout est clair maintenant !
-
mtschoon dernière édition par

De rien @mimims.
Contente que tout soit clair pour toi et bon travail.