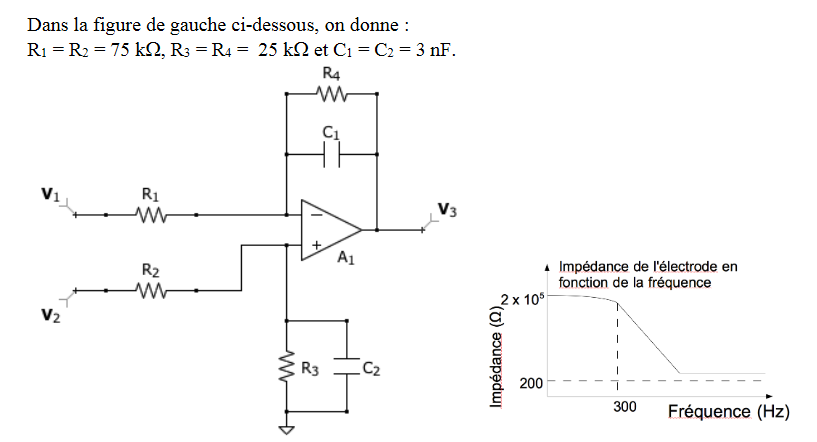
Amplification des signaux médicaux - Fonction de transfert

Bonjour pouvez-vous m'aider à commencer mon exercice parce que je ne sais pas par où partir.

Je dois commencer par calculer la fonction de transfert en considérant que l'entrée est donnée par V2-V1 et que la sortie est V3 en expliquant la démarche suivie.
Il faut décrire la fonction (=rôle) du circuit et si il y a lieu donner le gain et sa ou ses fréquences de coupures.

J'ai peut-être quelques idées sur la seconde question mais la première me laisse pour l'instant sans idées.

Merci par avance

Bonjour,

Soit Z1 = (R4//C1) et Z2 = (R3//C2)

V+/Z2 = V2/(R2 + Z2)
V+ = V2 * Z2/(R2+Z2)

I(R1) = (V1 - V-)/R1
Si on est dans la plage de régulation, V- = V+ (ampli considéré comme parfait)
I(R1) = (V1 - V2 * Z2/(R2+Z2))/R1
I(R1) = (V1*(R2+Z2) - V2Z2)/(R1(R2+Z2))

V3 = V- - Z1I1
V3 = V2 * Z2/(R2+Z2) - Z1(V1*(R2+Z2) - V2Z2)/(R1(R2+Z2))

V3 = V2 * (Z2/(R2+Z2) + Z1Z2/(R1(R2+Z2)) - V1 * Z1/R1

V3 = V2 * (1+(Z1/R1))/(1 +(R2/Z2)) - V1 * Z1/R1

Dans le cas de l'exercice (avec les valeurs numériques), on a Z2/R2 = Z1/R1 et alors :
(1+(Z1/R1))/(1 +(R2/Z2)) = (1+(Z1/R1))/(1 +(R1/Z1)) = (R1+Z1)Z1/(R1(Z1+R1)) = Z1/R1

---> V3 = (Z1/R1) * (V2 - V1)

et Z1 = (R4//C1) = (R4/(jwC1))/(R4 + 1/(jwC1)) = R4/(1+jwR4C1)

V3 = (V2 - V1) * (R4/R1) * 1/(1+jwR4C1)

V3/(V2-V1) = (R4/R1)/(1+jwR4C1)

V3/(V2-V1) = 1/(1 + j*7,5.10^-5.w)

C'est la fonction de transfert d'un Filtre passe bas ...

Bonjour @Black-Jack,

Premièrement je comprends bien pour Z1 et Z2.

Pour V+/Z2 je comprends les valeurs mais comment savez-vous (loi?) que V2/(R2+Z2)?

Je ne comprends pas à quoi correspond (ce que ça veut dire) I(R1).

Merci

@anesthesiste

Bonjour,

Pour V+/Z2 je comprends les valeurs mais comment savez-vous (loi?) que V2/(R2+Z2)

Simple diviseur de tension.

La tension aux bornes de Z2 est V+ (V+ étant la tension de l'entrée + de l'OP)
et V2 est la tension aux bornes de R2 en série avec Z2
et donc par diviseur de tension, on a directement : V+/Z2 = V2/(R2 + Z2)

Ou autrement :
Si on appelle i le courant qui entre dans R2, on a :
V2 =R2.i + Z2.i ---> i = V2/(R2+Z2)
et on a aussi V+ = Z2.i --> i = V+/Z2

et donc V+/Z2 = V2/(R2+Z2)

En se rappelant évidemment que le courant d'entrée dans l'OP (borne +) est nul (en considérant l'ampli parfait et travaillant dans sa zone de non saturation)

J'ai appelé I(R1) le courant passant dans la résistance R1 (flèche de gauche à droite sur le dessin)

Il faut aussi se rappeler que le courant d'entrée dans l'OP (borne -) est nul (en considérant l'ampli parfait et travaillant dans sa zone de non saturation)

OK ?

Bonjour @Black-Jack,
Oui c'est beaucoup plus clair merci.
Je vais maintenant essayer de voir la démarche dans son ensemble pour voir si je comprends bien et si j'arrive au même résultat

Edit:@Black-Jack

Dans sur V+, si on mesure la tension aux borne de Z2, c'est en raison des règles de l'AOP V+=V-=0 donc le courant passe forcément dans la branche Z2?

Par contre ça ne va pas dans le calcul de I(R1):

Est-ce qu'il ne faut pas faire en entrée V2-V1 comme indiqué dans l'énoncé?
Après bien qu'on utilise la loi d'Ohm je ne comprends pas ( à part le fait que R1 soit au dénominateur ça c'est OK).

J'avais répondu ... mais ma réponse est partie mystérieusement sur un autre post.

Je recopie ma réponse ici :

Bonjour @Black-Jack,
Oui c'est beaucoup plus clair merci.
Je vais maintenant essayer de voir la démarche dans son ensemble pour voir si je comprends bien et si j'arrive au même résultat

Edit:@Black-Jack

Dans sur V+, si on mesure la tension aux borne de Z2, c'est en raison des règles de l'AOP V+=V-=0 donc le courant passe forcément dans la branche Z2?

Par contre ça ne va pas dans le calcul de I(R1):

Est-ce qu'il ne faut pas faire en entrée V2-V1 comme indiqué dans l'énoncé?
Après bien qu'on utilise la loi d'Ohm je ne comprends pas ( à part le fait que R1 soit au dénominateur ça c'est OK).
Attention ...

V+=V-=0 n'est pas correct

On a V+ = V-

Mais V+ n'est pas nul et donc V- non plus.

Dans le cas des amplis inverseurs (montage très fréquent) , on met V+ à la masse (0 Volt)

et dans ce cas, si on travaille dans la zone linéaire (pas de saturation), on a bien V+ = V- = 0

Mais dans le montage de l'exercice, on ne met pas V+ à la masse, si on travaille dans la zone linéaire (pas de saturation), on a bien V+ = V- ... mais pas = 0

Par contre ça ne va pas dans le calcul de I(R1):

Est-ce qu'il ne faut pas faire en entrée V2-V1 comme indiqué dans l'énoncé?

Non.

Le potentiel à gauche de R1 est V1
Le potentiel à droite de R1 est V-

Donc la différence de potentiel (tension) aux bornes de R1 est (V1 - V-)
et la loi d'Ohm donne donc I(R1) = (V1 - V-)/R1

Bonjour @Black-Jack,

Comment savez-vous que l'AOP est dans une plage de régulation?

J'ai fais le calcul de I(R1) mais je n'obtiens pas le même résultat:

$v1∗(R2+Z2)−V2Z2R2+Z2R1\frac{v1*(R2+Z2) - V2Z2}{\frac{R2+Z2}{R1}}$

J'obtiens une divisions à trois étages donc j'ai envie de faire de manière conventionnelle:
V1 * (R2+Z2) - V2 Z2 * $R1R2+Z2\frac{R1}{R2+Z2}$

Mais là je n'obtiens pas le même résultat que vous.

Enfin dernière question est-ce que je peux dire à l'écrit que sur le circuit donnée on identifie 2 circuits RC ( Z1 et Z2)? Est-ce que c'est correct?

Merci par avance

@anesthesiste a dit dans Amplification des signaux médicaux - Fonction de transfert :

Bonjour @Black-Jack,

Comment savez-vous que l'AOP est dans une plage de régulation?

J'ai fais le calcul de I(R1) mais je n'obtiens pas le même résultat:

$v1∗(R2+Z2)−V2Z2R2+Z2R1\frac{v1*(R2+Z2) - V2Z2}{\frac{R2+Z2}{R1}}$

J'obtiens une divisions à trois étages donc j'ai envie de faire de manière conventionnelle:
V1 * (R2+Z2) - V2 Z2 * $R1R2+Z2\frac{R1}{R2+Z2}$

Mais là je n'obtiens pas le même résultat que vous.

Enfin dernière question est-ce que je peux dire à l'écrit que sur le circuit donnée on identifie 2 circuits RC ( Z1 et Z2)? Est-ce que c'est correct?

Merci par avance

Bonjour,

$v1∗(R2+Z2)−V2Z2R2+Z2R1\frac{v1*(R2+Z2) - V2Z2}{\frac{R2+Z2}{R1}}$

Ce n'est pas correct ...
Il suffit pour s'en convaincre de faire une équation aux dimensions (ou aux unités)

Le numérateur est en Volt * ohm
Le dénominateur est en ohm/ohm ... donc sans dimension
Le rapport est donc en Volt * ohm ... alors qu'il devrait être en Ampères (ou en Volt/ohm)

Si on reprend mon expression, soit :
I(R1) = (V1*(R2+Z2) - V2Z2)/(R1(R2+Z2))

Le numérateur est en Volt * ohm
Le dénominateur est en ohm * ohm ... donc ohm²

le rapport est en Volt * ohm/(ohm²) = Volt/ohm = ampère.

Ma relation est donc homogène ... cela ne prouve pas qu'elle est correcte.

Par contre, le fait que ta relation n'est pas homogène prouve que ta relation est obligatoirement fausse.

D'accord c'est quelque chose où je n'ai jamais étais familiarisé donc je suis content d'avoir vu cette notion de relation homogène.

Mais comment a partir de:

@Black-Jack a dit dans Amplification des signaux médicaux - Fonction de transfert :

Si on est dans la plage de régulation, V- = V+ (ampli considéré comme parfait)
I(R1) = (V1 - V2 * Z2/(R2+Z2))/R1

Mais comment à partir de là arriver à rendre la relation homogène?

@anesthesiste a dit dans Amplification des signaux médicaux - Fonction de transfert :

I(R1) = (V1 - V2 * Z2/(R2+Z2))/R1

Si on ne fait pas d'erreurs dans les raisonnements, on trouve des relations homogènes.

On peut vérifier que la relation trouvée est homogène ...
Si c'est le cas, l'expression est peut-être correcte.
Si ce n'est pas le cas, alors, à coup sûr l'expression est fausse.

I(R1) = (V1 - V2 * Z2/(R2+Z2))/R1

En Latex :
$IR1=V1−V2∗Z2R2+Z2R1I_{R_1} = \frac{V_1 - V_2* \frac{Z_2}{R_2+Z_2}}{R_1}$

$IR1=V1∗R2+Z2R2+Z2−V2∗Z2R2+Z2R1I_{R_1} = \frac{V_1 * \frac{R_2+Z_2}{R_2+Z_2} - V_2* \frac{Z_2}{R_2+Z_2}}{R_1}$

$IR1=V1∗(R2+Z2)−V2∗Z2(R2+Z2)∗R1I_{R_1} = \frac{V_1 * (R_2+Z_2) - V_2 * Z_2}{(R_2+Z_2) * R_1}$

@Black-Jack a dit dans Amplification des signaux médicaux - Fonction de transfert :

@anesthesiste a dit dans Amplification des signaux médicaux - Fonction de transfert :

I(R1) = (V1 - V2 * Z2/(R2+Z2))/R1

Alors si je comprends bien une fois qu'on a l'équation ci-dessus. Le but est de modifier "l'agencement" afin d'obtenir un rapport final en ampère?
J'aurais pensé spontanément que ça pouvait faire changer la valeur final de modifier l'emplacement des termes

@anesthesiste a dit dans Amplification des signaux médicaux - Fonction de transfert :

Alors si je comprends bien une fois qu'on a l'équation ci-dessus. Le but est de modifier "l'agencement" afin d'obtenir un rapport final en ampère?

Pas du tout, n'importe quelle ligne du développement pour I(R1) = ... donne des ampères.
C'est juste une "mise en forme" qui facilite l'écriture, rien d'autre.

Tu cherches des problèmes là où il n'y en a pas.

Le but (imposé par l'énoncé) est de trouver la fonction de transfert écrite sous la forme V3/(V2-V1) = ...

J'ai montré que ce n'était possible que dans le cas où Z2/R2 = Z1/R1 (ce qui est le cas avec les valeurs numériques données).
Et donc sous la condition d'avoir Z2/R2 = Z1/R1 , la fonction de transfert est :
V3/(V2-V1) = (R4/R1)/(1+jwR4C1)

On peut arriver à cela en menant les calculs par de multiples moyens...
J'en ai montré un.

Tu peux, à partir du schéma (et sous les conditions données), mener des calculs comme tu veux ... et à conditions de ne pas faire d'erreur, tu dois arriver à la même finale, soit la relation : V3/(V2-V1) = (R4/R1)/(1+jwR4C1)

On peut ne pas passer par le calcul de I(R1) si on veut et utiliser d'autres méthodes (par exemple en utilisant Millman), peu importe ... mais il faut arriver à la solution finale.

@Black-Jack
Merci @Black-Jack, pour cette explication que j'ai compris.

Je valide aussi le fait qu'il s'agisse d'un filtre passe-bas qui fait sens pour la question 2.
Cette question demande aussi si il y a lieu de donner le gain du circuit ou de sa/ses fréquences de coupure.
Concernant la fréquence de coupure j'ai envie de dire que avec le petit schéma présent à côté du circuit la fréquence de coupure est à 300 Hz mais si c'est le bon résultat y-a-t-il une formule pour la vérifier?

Et là aussi si possible y-a-t-il une formule pour calculer le gain?

Merci et bonne soirée

Bonjour,

Attention,

"le petit schéma présent à côté du circuit" est l'impédance de l'électrode que l'on connectera à l'entrée de l'ampli... donc 300 Hz n'est pas la fréquence de coupure de l'ampli.

A partir de V3/(V2-V1) = 1/(1 + j*7,5.10^-5.w), tu dois pouvoir trouver le gain de l'ampli et sa fréquence de coupure.

De manière générale, une fonction de transfert H(w) = K/(1 + jwT)
a un gain K et une pulsation de coupure wo = 1/T, avec wo = 2Pi.fo (fo en Hz est la fréquence de coupure)

Sauf erreur on a : K = 1 (gain) et fo = 2122 Hz

Remarque :

Sans avoir l'énoncé complet de l'exercice, il est difficile de juger de sa pertinence.

Si on branche directement l'électrode à l'entrée de l'ampli, la fonction de transfert de l'ensemble sera très différente. De plus, avoir un ampli avec un gain de 1, quand on sait que l'amplitude des signaux sortant de la plupart des électrodes médicales est très petite ... il y a comme un soucis.
Mais pas possible d'en dire plus sans autres informations.

Bonjour @Black-Jack ,

Ça me paraissait un peu simple le schéma donnant directement la fréquence de coupure, je comprends mieux la raison de sa présence maintenant.

Je n'arrive pas à faire le calcul du gain pour trouver la valeur 1 (y a t il une unité? j'avais entendu parlé de gain ou dB ou autre)
EDIT: En fait il n'y a pas de calcul à faire c'est juste une lecture de la fonction de transfert?

Pour la fréquence de coupure et suite à vos explications je fais:

2PI*fo = 1/T
$fo=1T2PIfo=\frac{1}{\frac{T}{2PI}}$

Mais je n'arrive pas à identifier T dans la fonction de transfert, est-ce que c'est parce que T=1 et qu'il n'apparait pas dans la fonction de transfert?

Merci

@Black-Jack a dit dans Amplification des signaux médicaux - Fonction de transfert :

1/(1 + j*7,5.10^-5.w)

C'est pourtant élémentaire.

Il suffit de comparer : 1/(1 + j*7,5.10^-5.w)
et K/(1 + jwT)

On a directement K = 1 et T = 7,5.10^-5 s
wo = 1/T = 13333 rad/s
fo = wo/(2Pi) = 2122 Hz

Si on veut le gain en dB, le diagramme asymptotique (gain en dB en ordonnées) et log(f) en abscisse ...
On a une horizontale à log(K) = log(1) = 0 dB jusque f = fo et ensuite, le gain descend avec une pente de 20 dB/décade.

Pas sûr que cela soit demandé dans l'exercice.

Bonjour @Black-Jack
C'est très clair j'ai compris.

Merci à vous

Bonjour,

Alors je viens de refaire l'exercice et j'aurais besoin de quelques précisions.

Pour V3: j'ai aussi mis V- - Z1/R1
Bien que cela soit en adéquation avec la correction donnée, je ne suis pas sur de comprendre pourquoi - (celui en gras).

Après pour le calcul de V3, je suis bloqué à

@Black-Jack a dit dans Amplification des signaux médicaux - Fonction de transfert :

V3 = V2 * Z2/(R2+Z2) - Z1*(V1*(R2+Z2) - V2Z2)/(R1(R2+Z2))

Après cela impossible d'arriver aux calculs suivants:

V3 = V2 * (Z2/(R2+Z2) + Z1Z2/(R1(R2+Z2)) - V1 * Z1/R1

V3 = V2 * (1+(Z1/R1))/(1 +(R2/Z2)) - V1 * Z1/R1

Bonne journée

@anesthesiste a dit dans Amplification des signaux médicaux - Fonction de transfert :

Bonjour,

Alors je viens de refaire l'exercice et j'aurais besoin de quelques précisions.

Pour V3: j'ai aussi mis V- - Z1/R1
Bien que cela soit en adéquation avec la correction donnée, je ne suis pas sur de comprendre pourquoi - (celui en gras).

Après pour le calcul de V3, je suis bloqué à

@Black-Jack a dit dans Amplification des signaux médicaux - Fonction de transfert :

V3 = V2 * Z2/(R2+Z2) - Z1*(V1*(R2+Z2) - V2Z2)/(R1(R2+Z2))

Après cela impossible d'arriver aux calculs suivants:

V3 = V2 * (Z2/(R2+Z2) + Z1Z2/(R1(R2+Z2)) - V1 * Z1/R1

V3 = V2 * (1+(Z1/R1))/(1 +(R2/Z2)) - V1 * Z1/R1

Bonne journée

Tu ne peux pas bloquer sur des calculs aussi élémentaires.

$\frac{Z2}{R2+Z2} - Z1 * \frac{V1 * (R2+Z2) - V2 * Z2}{R1(R2+Z2)}$

$\frac{Z2}{R2+Z2} + V2 * \frac{Z1Z2}{R1(R2+Z2)} - Z1 * V1 * \frac{R2+Z2}{R1(R2+Z2)}$

$(\frac{Z2}{R2+Z2} + \frac{Z1Z2}{R1(R2+Z2)}) - V1 * \frac{Z1}{R1}$

$(\frac{Z2}{R2+Z2} * (1 + \frac{Z1}{R1})) - V1 * \frac{Z1}{R1}$

$(\frac{1}{1 + \frac{R2}{Z2}} * (1 + \frac{Z1}{R1})) - V1 * \frac{Z1}{R1}$

$\frac{1 + \frac{Z1}{R1}}{1 + \frac{R2}{Z2}} - V1 * \frac{Z1}{R1}$

Bonjour @Black-Jack ,

Merci pour le détail je vais reprendre ça et surement les bases qui vont avec.

Je suppose que c'est la même logique pour les valeurs numériques car:

@Black-Jack a dit dans Amplification des signaux médicaux - Fonction de transfert :

V3/(V2-V1) = (R4/R1)/(1+jwR4C1)

V3/(V2-V1) = 1/(1 + j*7,5.10^-5.w)

Vous mettez que R4/R1 =1, je ne dois pas faire comme il faut car je remplace par les valeurs données comme (25/75)
en plus je suppose qu pour le numérateur il y a une conversion à faire car on a des KOhm avec des nF?

Bon Week end

@anesthesiste

Bonjour,

J'ai mal lu les données numériques.

V3/(V2-V1) = (R4/R1)/(1+jwR4C1)
V3/(V2-V1) = (1/3)/(1+jw * 25000 * 3 * 10^-9)
V3/(V2-V1) = (1/3)/(1+jw * 7,5.10^-5)

Gain(DC) : K = 1/3
fo = 2122 Hz

Si on veut le gain en dB, le diagramme asymptotique (gain en dB en ordonnées) et log(f) en abscisse ...
On a une horizontale à 20 * log(K) = 20 * log(1/3) = -9,5 dB jusque f = fo et ensuite, le gain descend avec une pente de 20 dB/décade.

Sauf nouvelle distraction.

Ce message a été supprimé !

Bonjour @Black-Jack
Merci pour votre réponse.
Je voulais aussi m'assurer de l'équation de V3:
Sommes nous d'accord que :
V3= (v-)-(Z1*R1)/R1 ?
@Black-Jack a dit dans Amplification des signaux médicaux - Fonction de transfert :

V3 = V- - Z1/1

Pour le reste cela correspond à ce que j'ai trouvé de mon côté.

Excellent dimanche