Points critiques + Min/Max/Point selle

Bonjour,
Il me faut trouver 4 points critiques pour cette fonction + si c'est un max, min, ou point selle :
f(x,y) = x^3 +3x^2-3x^2-3y^2+10

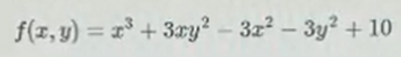
Merci d'avance.

@Rémy-E a dit dans Points critiques + Min/Max/Point selle :

Bonjour,
Il me faut trouver 4 points critiques pour cette fonction + si c'est un max, min, ou point selle :
f(x,y) = x^3 +3x^2-3x^2-3y^2+10

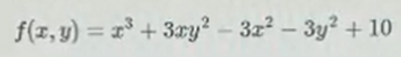
@Rémy-E , bonjour,

Je pense que tu t'es trompé de rubrique car cet énoncé n'est pas au programme de Terminale S.
La modération le déplacera éventuellement.

@Rémy-E , je te mets quelques pistes pour démarrer.

$f(x,y)=x^3+3xy^2-3x^2-3y^2+10$

Regarde ton cours.
Tu dois calculer les dérivées partielles
$δfδx(x,y)=3x2−6x+3y2\dfrac{\delta f}{\delta x}(x,y)=3x^2-6x+3y^2$
$δfδy(x,y)=6xy−6y\dfrac{\delta f}{\delta y}(x,y)=6xy-6y$

Les points critiques sont solutions du système :
${3x2−6x+3y2=06xy−6y=0\begin{cases}3x^2-6x+3y^2=0\cr 6xy-6y=0\end{cases}$

Sauf erreur, après résolution, tu dois trouver 4 points critiques
$(2, 0), (1, 1), (1, - 1), (0, 0)$

Ensuite, tu dois avoir des théorèmes dans ton cours.

Soit a est un point critique de f
Tu calcules
$r=\dfrac{\delta^2 f}{\delta x^2}(a)$

$s=\dfrac{\delta^2 f}{\delta x \delta y}(a)$

$t=\dfrac{\delta^2 f}{\delta y^2}(a)$

Tu distingue les cas :

Si rt−s²>0 et r>0, f admet un minimum relatif en a.
Si rt−s²>0 et r<0, f admet un maximum relatif en a.
Si rt−s²<0, f n'admet pas d'extremum en a, il y a un point selle.
Si rt−s²=0, on ne peut pas conclure.

Bons calculs .

@mtschoon Oui effectivement, n'habitant pas en France je ne connais rien à vos systèmes universitaires/collégiaux Merci quand même pour ta réponse !

Ce message a été supprimé !

Merci
Ce n'était vraiment pas si compliqué.

De rien @LiamOgden

Il fallait maîtriser le cours, surtout.

Bon travail à toi et à@Rémy-E

@mtschoon J'ose encore te demander comment tu as trouvé les 4 points critiques ?
Merci d'avance.

@Rémy-E

Bonjour,

Recherche des points critiques.

On écrit le système correspondant à l'annulation des dérivées partielles premières de f par rapport à x et à y.

On arrive au système :

3x²-6x+3y² = 0
6xy-6y = 0

x²-2x+y² = 0
xy - y = 0

x²-2x+y² = 0 (1)
y.(x-1) = 0 (2)

(2) --> y = 0 OU x = 1

Si y = 0, (1) --> x²-2x = 0
x(x-2) = 0 et donc x = 0 ou x = 2

Les points de coordonnées (0 ; 0) et (2 ; 0) sont des points critiques.

Si x = 1, (1) --> -1 = y²
y² = 1
y = -1 OU y = 1

Les points de coordonnées (1 ; -1) et (1 ; 1) sont des points critiques.

Il y a donc 4 points critiques, ils ont pour coordonnées (0 ; 0) , (2 ; 0) , (1 ; -1) et (1 ; 1)

@Rémy-E a dit dans Points critiques + Min/Max/Point selle :

@mtschoon J'ose encore te demander comment tu as trouvé les 4 points critiques ?
Merci d'avance.

Tu peux oser @Rémy-E !
Comme Black-Jack vient de faire les calculs, je ne les refais pas.
Je pense qu'ils vont te convenir.

@Black-Jack @mtschoon Merci beaucoup ! J'ai effectivement un peu de peine avec ce genre d'exercices... mais avec un développement comme le vôtre je commence à comprendre la méthodologie

@Rémy-E , c'st le but que tu comprennes !
Nous faisons au mieux.
Bon travail.

Bonsoir,

Merci à la modération d'avoir déplacer le topic car, en France, les fonctions à deux variables ne s'étudient qu'en Post Bac.