Théorème oral de mathématiques

Bonjour tout le monde! Je suis nouvelle sur le forum et j'ai quelques souci pour préparer un oral de mathématiques. Je dois utiliser principalement les théorème de Pythagore, Cercle de Thalès, l'angle inscrit et l'angle au centre mais pas de calcul à la calculatrice. J'ai réussi à en résoudre plusieurs mais certains dont celui-ci me posent encore problème.
Comme je n'ai pas le droit de poster l'image, je vais essayer de la décrire: il s'agit d'un cercle de centre O. Une tangente AT passe au point T sur le cercle et une deuxième tangente AT' passe au point T' sur le cercle et ces deux tangentes se rejoignent au point A. Trois rayons TO, T'O et T''O sont dessinés (Dont TO et T'O semblent être perpendiculaire aux tangentes mais aucune indication sur ce schéma). Une troisième tangente coupe la tangente AT au point B et coupe la tangente AT' au point C. Le rayon T''O semble aussi être perpendiculaire à la tangente BC mais de nouveau, il n'y a pas d'indication.
La question: Que vaut le périmètre du triangle ABC si l'on connait la mesure de AT?

Ce sera peut-être plus simple avec le schéma si cela est autorisé sur ce forum. [texte du lien]( 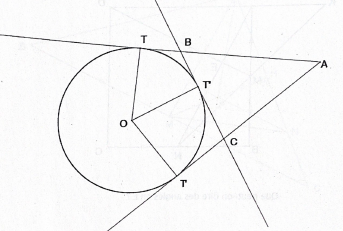Screenshot 2021-06-12 at 12.27.02.png url du lien)

@Flo-Flo , bonjour,

Tout d'abord quelques propriétés relatives aux tangentes qui seront utiles dans les calculs.

Toute tangente est perpendiculaire au rayon issu du point de contact.
$\perp (TA)$
$(OT′)⊥(T′A)(OT')\perp (T'A)$
$(OT′′)⊥(BC)(OT'')\perp(BC)$
Tu peux compléter le schéma en traçant $(O A), (O B), (O C)$ .
Les points $T$ et $T^{''}$ sont symétriques par rapport à $(O B$ )
Les points $T^{'}$ et $T^{''}$ sont symétriques par rapport à $(O C$ )
Les points $T$ et $T^{'}$ sont symétriques par rapport à $(O A$ )
D'où les égalités :
$B T = B T^{''}$ , $C T^{'} = C T^{''}$ , $A T = A T^{'}$

CALCULS

$A B = A T - T B = A T - B T^{''}$
$A C = A T^{'} - T^{'} C = A T - C T^{''}$

En ajoutant membre à membre ces deux égalités :
$A B + A C = A T - B T^{''} + A T - C T^{''} = 2 A T - (B T^{''} + C T^{''})$
Donc :
$A B + A C = 2 A T - B C$
En transposant $B C$ dans le membre de gauche :
$AB+AC+BC=2AT\boxed{AB+AC+BC=2AT}$
Le périmètre du triangle $A B C$ vaut donc $2 A T$

Remarque : Pour un oral, tout dépend du temps de la recherche...
Je trouve que cet exercice, même si les calculs sont très simples, n'est pas si simple que ça, car il faut le temps pour trouver la stratégie utile.