quadrilatère ABCD - théorèmes de l'angle inscrit,Thalès,Pythagore

Hello tout le monde! Voici un exercice d'entraînement pour mon oral de mathématiques. A partir de la forme proposée, je dois utiliser les différents théorèmes (Thalès, Pythagore, angle inscrits notamment) pour pouvoir en déduire qqch sur le quadrilatère ABCD. (Que peut-on dire du quadrilatère ABCD?)
Voici la forme donnée: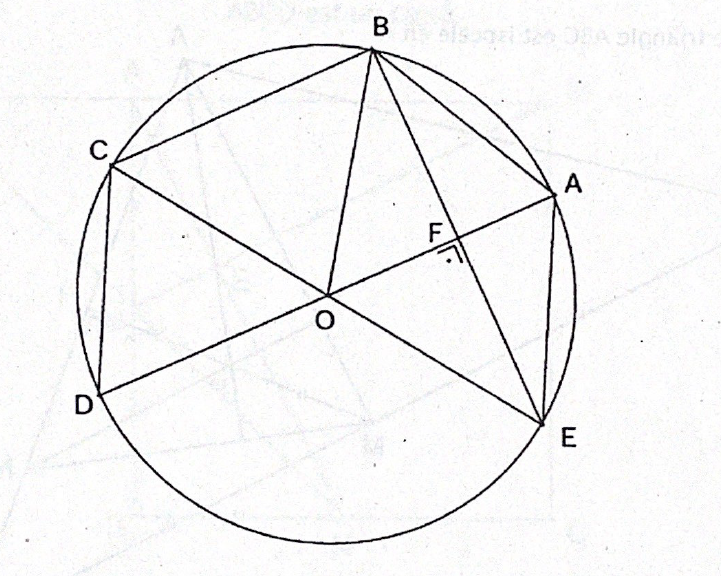 Screenshot 2021-06-12 at 13.49.18.png
J'imagine qu'il va falloir prouver que c'est un trapèze isocèle, et qu'il y aura donc deux côtés égaux avec des angles égaux aussi. Mais le chemin pour arriver à cette conclusion? Je ne vois pas...
Aussi, j'ai lu: Dans tout quadrilatère inscrit dans un cercle, la somme des angles en A et C, comme celle des angles en B et D vaut 180°. Est-ce que cela signifie que l'angle en A + l'angle en C = 180° et donc que les 4 angles valent 360°?
J'ai aussi lu: L’angle C et l’angle A sont égaux et valent les deux la moitié de l’angle O. L'angle C est la moitié de l'angle O ou est-ce que cela signifie: les angles (C+A) valent la moitié de l'angle O?
Si vous avec des éclaircissements à me fournir, je suis preneuse! Merci mille fois!! F.

@Flo-Flo , bonjour,

Quelques pistes possibles pour justifier que $A B C D$ est un trapèze isocèle.

D'après l'indication du schéma $\bot (BE)$

Lorsqu'on joint une point d'un cercle aux extrèmités d'un diamètre, on forme un angle droit, donc $CBE^\widehat{CBE}$ est droit, donc $\bot (BE)$

Les droites $(D A$ ) et $(C B$ ) sont perpendiculaires à une même droite $(B E)$ , donc elles sont parallèles entre elles : $(C B) / / (D A)$

Le quadrilatère ABCD est donc un trapèze.

Pour montrer que $A B = C D$ , tu peux comparer les triangles $O A B$ et $O C D$ et prouver qu'ils sont égaux.

Tu as déjà $O A = O B = O C = O D$ (rayons du cercle)

Ensuite, tu peux comparer les angles.

Le triangle $O B C$ et isolèle (vu que $O B = O C$ )
Donc les angles $OBC^\widehat{OBC}$ et $OCB^\widehat{OCB}$ sont égaux

$OBC^=BOA^\widehat{OBC}=\widehat{BOA}$ comme angles appelés "alternes-internes", vu que les droites $(B C)$ et $(A D)$ sont parallèles.
De même , pour la même raison $OCB^=COD^\widehat{OCB}=\widehat{COD}$

Donc $BOA^=COD^\widehat{BOA}=\widehat{COD}$

Conclusion : les triangles $A O B$ et $C O D$ ont une angle repectivement égal compris entre deux côtés respectivement égaux, donc ils sont égaux
Donc : AB=CD

Le quadrilatère ABCD est un trapèze isocèle.

Remarque : j'espère que les notions utilisées font partie de ton programme...

Bonjour @mtschoon! Je vous remercie énormément pour votre aide ainsi que votre rapidité!! Mille merci, vos explications sont très claires! Bon week-end! Flo

De rien @Flo-Flo et bon entraînement !