Racine carrée et valeur absolue
-
ABCD EFGH dernière édition par

J'ai une question qui me gêne toujours , est-ce que √(x)^2 = (√x)^2 et merci d'avance
-
BBlack-Jack dernière édition par
Bonjour,
C'est pas clair.
S'agit-il de V(x²) = (V(x))² ?
Si oui, alors c'est faux lorsque x < 0, car le membre de gauche existe et le membre de droite n'existe pas.
-
ABCD EFGH dernière édition par

@Black-Jack ah non c'est le symbole de la racine carrée désolé
-
BBlack-Jack dernière édition par
@ABCD-EFGH a dit dans Racine carrée et valeur absolue :
@Black-Jack ah non c'est le symbole de la racine carrée désolé
Ben oui, cela je l'avais bien compris.
Moi j'ai écris V à la place du symbole racine carrée, mais soit.Ce qui n'est pas clair dans ton message est ceci : √(x)^2
Ecrit ainsi, on ne peux pas savoir si cela correspond à (√(x))^2 ou bien à √((x)^2)
Et c'est bien là qu'il y a un soucis car : (√(x))^2 n'existe pas si x < 0 alors que √((x)^2) existe quel que soit le signe de x
-
BBlack-Jack dernière édition par
Je recommence ma réponse initiale en Latex.
C'est pas clair.
S'agit-il de x2=(x)2\sqrt{x^2} = (\sqrt{x})^2x2=(x)2 ?
Si oui, alors c'est faux lorsque x < 0, car le membre de gauche existe et le membre de droite n'existe pas.
-
mtschoon dernière édition par mtschoon

Bonjour,
x2=(x)2\boxed{\sqrt{x^2}=(\sqrt x)^2}x2=(x)2 ?
@ABCD-EFGH , comme déjà indiqué, dans l'ensemble des réels, on ne peux prendre la racine carrée que d'un nombre positif, donc pour x<0x\lt 0x<0, le membre de droite n'existe pas alors que le membre de gauche existe car dans ce cas x2>0x^2\gt 0x2>0, donc égalité proposée impossible.
Bien sûr, l'égalité est vraie pour x≥0x\ge 0x≥0
Vu que tu postes généralement en Terminale, tu dois bien savoir que la racine carré du produit de deux nombres positifs est égal au produit de leurs racines carrées respectives.Pour a≥0a\ge 0a≥0 et b≥0b \ge 0b≥0 : a×b=a×b\sqrt{a\times b}=\sqrt a \times \sqrt ba×b=a×b
En posant a=b=xa=b=xa=b=x, tu obtiens donc
x×x=x×x\sqrt{x\times x}=\sqrt x \times \sqrt xx×x=x×x, c'est à dire :
x2=(x)2\sqrt{x^2}=(\sqrt x)^2x2=(x)2Bonne réflexion.
-
mtschoon dernière édition par mtschoon

@ABCD-EFGH , je regarde ton titre "Racine carrée et valeur absolue"
Si tu veux écrire une égalité valable pour tout x réel, tu peux écrire :
x2=(∣x∣)2\boxed{\sqrt{x^2}=\biggl(\sqrt{|x|}\biggl)^2}x2=(∣x∣)2Le plus simple est bien sûr d'écrire :
Pour tout x réel , x2=∣x∣\boxed{\sqrt {x^2}=|x|}x2=∣x∣Demande si tu as besoin d'une justification.
-
mtschoon dernière édition par

Pour illustration, je te mets les représentations graphiques (confondues) des fonctions f, g, h, définies sur R.
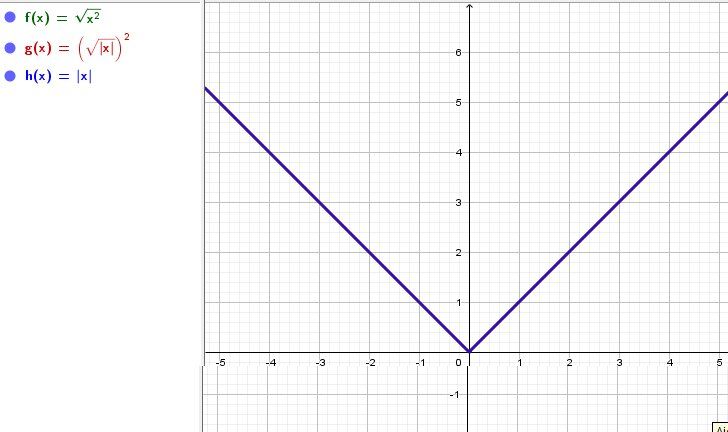
-
ABCD EFGH dernière édition par

@mtschoon merci infiniment , vraiment là j'ai bien compris, "je ne me suis pas connecté depuis que j'ai posté la question donc c'est juste maintenant que j'ai vu votre explication " sinon merci beaucoup
-
ABCD EFGH dernière édition par

@Black-Jack oui c'est ça merci beaucoup j'ai bien compris
-
mtschoon dernière édition par mtschoon

@ABCD-EFGH , de rien !
Nous faisons le mieux possible.
C'est parfait si tu as bien compris. C'est le but !
Bon travail.