Définition de ordonnée a l'origine et de racine

Bonjour à tous et à toutes
Dans quelques jours je vais avoir un "examen" et pour être sûre de mes définitions les voici:
Racine: La racine d'une fonction est un réel dont l'image par cette fonction est nulle
Ordonnée à l'origine: L'ordonnée à l'origine est l'image par la fonction du réel 0.
Voila je voulait juste savoir si ces 2 définition étais +- cohérente
Merci

@ARK_Toex_ , bonjour,

Oui, tes définitions conviennent.

Si f est une fonction de la variable x dont tu connais la représentation graphique, les racines sont les abscisses des points d'intersection de la courbe avec l'axe des abscisses, c'est à dire les valeurs de x telles que f(x)=0

exemple : soit $f (x) = 2 x + 3$

$f (x) = 0$ <=> $2 x + 3$ =0 <=> $2 x = - 3$ <=> $x=−32x=-\dfrac{3}{2}$

$−32-\dfrac {3}{2}$ est la racine de f

Si f est une fonction de la variable x dont tu connais la représentation graphique, l'ordonnée à l'origine est l'ordonnée du point d'intersection de la courbe avec l'axe des ordonnées, c'est à dire la valeur de f(0)

exemple : $f (x) = 2 x + 3$

$f (0) = 2 (0) + 3 = 3$

3 est l'ordonnée à l'origine de f

Représentation graphique de f définie par $f(x)=2x+3\boxed{f(x)=2x+3}$

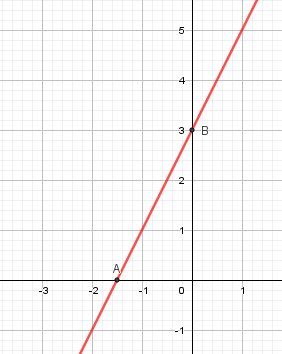
A a pour abscisse $−32=−1.5-\dfrac{3}{2}=-1.5$
B a pour ordonnée 3.

D'accord un grand merci

De rien @ARK_Toex_ et bonnes révisions pour ton examen .