Probabilité conditionnelle formalisation
-
Lloicstephan dernière édition par loicstephan
Une entreprise reçoit un lot de pièces détachées qui peut
comporter un certain nombre de pièces défectueuses. En
présence de pièces défectueuses, le lot est dit défectueux et il est rejeté. On admet que la probabilité qu' une pièce
soit défectueuse est égale à 5 %. Afin de décider si l'on
doit ou non accepter un lot, l'entreprise met en place une
procédure de détection. Les résultats de cette procédure
montrent que si le lot est défectueux, le test conduit au
rejet du lot avec une probabilité de 98 %. Lorsque le lot
est effectivement non défectueux, le test conduit (à tort)
au rejet du lot avec une probabilité de 4 %.- Quelle est la probabilité qu'un lot soit effectivement
défectueux si le test conduit au rejet du lot ? - Quelle est la probabilité qu' un lot soit valide si le test
conduit au rejet du lot ? - Quelle est la probabilité qu' un lot soit défectueux si
le test ne conduit pas au rejet du lot? - Quelle est la probabilité qu' un lot soit valide si le test
ne conduit pas au rejet du lot?
personellement je bloque sur la fomalisation du proble. je joins ainsi l'arbre que j'ai essayé de faire!
je trouve l'independance entre les evennements du coup
P(D/R)=DP(D/R) = D P(D/R)=D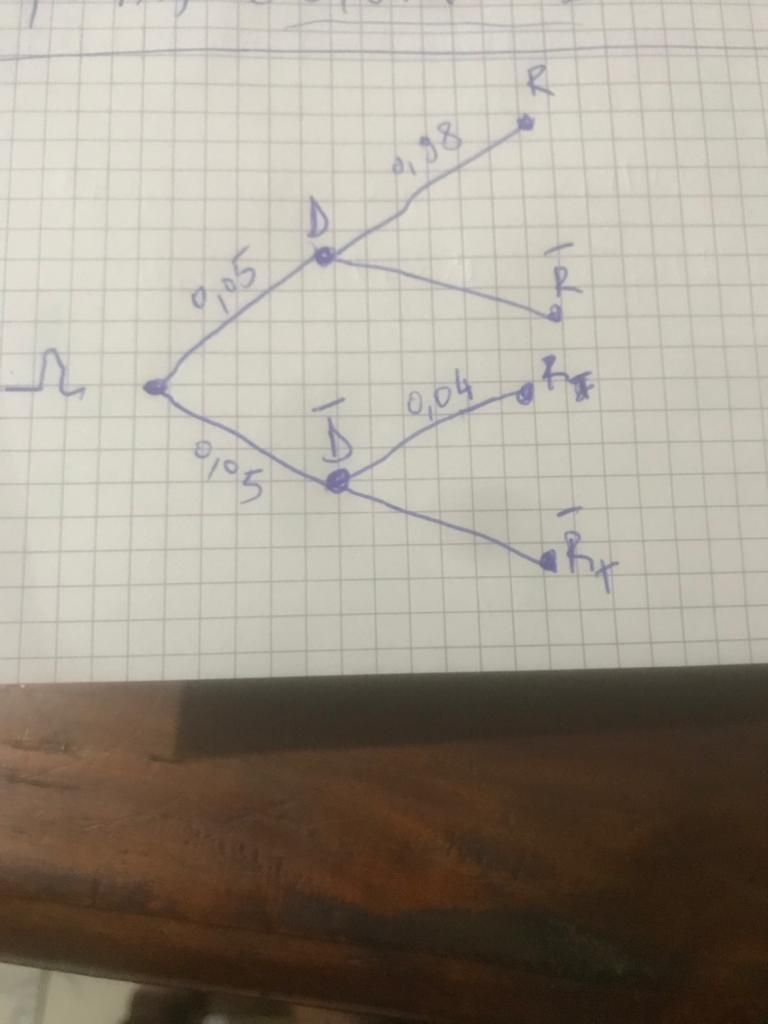
en essayant de raisonner avec mon arbre il y a des probailités absentes je suis un peu bloqué!
- Quelle est la probabilité qu'un lot soit effectivement
-
mtschoon dernière édition par mtschoon

Je regarde ton arbre.
Il y a une erreur pour la probabilité de D‾\overline{D}D
Vu que p(D)=0.05p(D)=0.05p(D)=0.05, l'évènement contraire D‾\overline{D}D à la probabilité 1−p(D)=1−0.05=0.951-p(D)=1-0.05=0.951−p(D)=1−0.05=0.95
Pour les deux branches où tu n'as pas indiqué de probabilité, c'est pareil : il s'agit de la probabilité de l'évènement contraire
pD(R‾)=1−0.98=0.02p_{D}(\overline {R})=1-0.98=0.02pD(R)=1−0.98=0.02
pD‾(R‾)=1−0.04=0.96p_{\overline D}(\overline {R})=1-0.04=0.96pD(R)=1−0.04=0.96Ensuite, pour épondre aux questions, il te suffira de faire les calculs avec l'arbre.
-
Lloicstephan dernière édition par
ah madame ustement l'arbre n'est pas le soucis c'est les calculs por la question 1
il s'agit de P(D/R)oualorsP(D/R)P(D/R) ou alors P(D/R)P(D/R)oualorsP(D/R)
moi j'interprere comme etant la proba de defaut sachat qu'il y a eu rejet !
en d'autre termes P(D∩R)P(R)\frac{P(D \cap R)}{P(R)}P(R)P(D∩R) coontrairement par exeple au bac France métropolitaine 2013 ici il y a un chemin pour R et l'evennement R semble ne pas etredifferent de P(D∩R)P(D \cap R)P(D∩R) par exemple
-
mtschoon dernière édition par

@loicstephan , bonsoir
@loicstephan a dit dans Probabilité conditionnelle formalisation :
en essayant de raisonner avec mon arbre il y a des probailités absentes je suis un peu bloqué!
Vu ta question, il semblait que c'était les "probabilités absentes " ton souci ...
Si ce sont les questions, je regarderai demain.
-
Lloicstephan dernière édition par
en effet au moment ou je poste le sujet j'ai des difficultés a formaliser
cependant entre temps j'ai reussi mais je bute sur les questions exactement comme expliquées plus haut !
-
mtschoon dernière édition par mtschoon

@loicstephan , bonjour,
Je mets un arbre complet pour plus de clarté car les calculs , en totalité, utilisent l'arbre.
D‾\overline DD est nommé nonD
R‾\overline RR est nommé nonR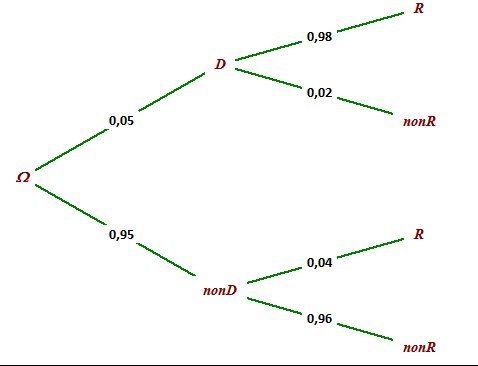
-
mtschoon dernière édition par

Je regarde la première question.
Probabilité donditionnelle
La condition commence par si........Tu dois donc chercher PR(D)P_R(D)PR(D)
PR(D)=P(D∩R)P(R)P_R(D)=\dfrac{P(D\cap R)}{P(R)}PR(D)=P(R)P(D∩R)
Avec l'arbre :
P(D∩R)=0.05×0.98P(D\cap R)=0.05\times 0.98P(D∩R)=0.05×0.98
P(R)=(0.05×0.98)+(0.95×0.04)P(R)=(0.05\times 0.98)+(0.95\times 0.04)P(R)=(0.05×0.98)+(0.95×0.04)Tu comptes .
Sauf erreur, tu dois trouver PR(D)≈0.563218P_R(D)\approx 0.563218PR(D)≈0.563218Pour la question 2), de la même façon, tu dois calculer PR(D‾)P_R(\overline D)PR(D)
Pour la question 3), de la même façon, tu dois calculer PR‾(D)P_{\overline R}(D)PR(D)
Pour la question 4), de la même façon, tu dois calculer PR‾(D‾)P_{\overline R}(\overline D)PR(D)
Tu peux donner tes réponses si tu souhaites une vérification.
-
Lloicstephan dernière édition par
bonjous tres chere
en suivant cette logique cela signifi qu'il y a pas de difference entre les evennement rejet a tort et rejet tout simplement!
je suis un peu perplexe!
-
mtschoon dernière édition par mtschoon

L'énoncé indique :
" Lorsque le lot est effectivement non défectueux, le test conduit (à tort) au rejet du lot avec une probabilité de 4%"Evidemment, dans l'absolu, lorsque le lot est effectivement non défectueux, le test devrait conduire au rejet du lot avec **une probabilité nulle (de 0%") **
C'est pour cela que l'énoncé indique ('à tort') (pour signaler l'anomalie de la chose...), mais cela n'intervient pas dans les calculs.En bref, ce genre d'exercice classique permet d'anayser la valeur du test qui n'est pas parfait . C'est le but !
-
Lloicstephan dernière édition par
@mtschoon a dit dans Probabilité conditionnelle formalisation :
(à tort)
merci bcp
en realte c'est donc du meme evennement qu'il s'agit! mais comme il est effectue a tort il est affecte de la probabilite indiquée!je vous joins les reponses aus questions dans un instant!
-
Lloicstephan dernière édition par loicstephan
1- P(D/R)=(0.98∗0.05)(0.98∗0.05)+(0.95∗0.04)=0.0490.087=0.56P(D/R)= \frac{(0.98 * 0.05)}{(0.98 * 0.05)+(0.95*0.04)} =\frac{0.049}{0.087}=0.56 P(D/R)=(0.98∗0.05)+(0.95∗0.04)(0.98∗0.05)=0.0870.049=0.56
2- P(Dˉ/R)=(0.95∗0.04)(0.98∗0.05)+(0.95∗0.04)=0.44P(\bar{D} / R) = \frac{(0.95 * 0.04)}{(0.98 * 0.05)+(0.95*0.04)} = 0.44P(Dˉ/R)=(0.98∗0.05)+(0.95∗0.04)(0.95∗0.04)=0.44
3-P(D/Rˉ)=(0.05∗0.02)(0.05∗0.02)+(0.95∗0.96)=0.0010.913=0.00109P(D/ \bar{R})= \frac{(0.05 * 0.02)}{(0.05 * 0.02)+ (0.95 * 0.96)}= \frac{0.001}{0.913}=0.00109 P(D/Rˉ)=(0.05∗0.02)+(0.95∗0.96)(0.05∗0.02)=0.9130.001=0.00109
4- onchercheP((Dˉ/Rˉ)on cherche P((\bar{D} / \bar{R})onchercheP((Dˉ/Rˉ) par le meme raisonnement on trouve 0.9980.9980.998
sauf erreur de ma part je crois que c'est correct!
-
mtschoon dernière édition par
