Loi conjointe du couple probabilité
-
Lloicstephan dernière édition par
Bonsoir a tous @Noemi @mtschoon
dans un super marche, 50 % des clients reglent leurs ahats avec des cheques, 40 % reglent en espece et 10 % avec carte bancaire.
on choisit deux clients. soit X e nombre de clients parmi les deux qui reglet avec des cheques et Y le nombre de clients parmi les deux qui paie en espece- calcler la loi conjoite du couple (X Y)
a- les loies marginales X et Y et leurs caracteristique (esperence et ecart type)
b- la loi conditionnelle de Y/X et ses caracteristiques
3 )
a- la fonction generatrice bivariee des moments du couple (X Y) et en deduire la covariance cov(X Y)
b- le coefficient de correlation lineaire r(X Y) et interpreter
4) deerminer la loi de probabilité des clients payant en espece sachant qu'un des clients a paye en par carte bancairemerci de m'aider car je suis habitue pour cet exerci a des tableaux aec des valeur a contingenter avant d'obtenir les probailites
ici j'arrive pas a determiner les valeurs de X et Y et le prabailite des couple respectifs
-
mtschoon dernière édition par mtschoon

@loicstephan , bonjour,
Je te donne quelques pistes sur la loi conjointe (avec lois marginales) pour que tu puisses ensuite traiter ton exercice.
Pour chaque client du super-marché, la probabilité de payer par chèque est 0,5, celle de payer en espèce est 0.4 et celle de payer par carte est 0.1
Soit a et b les deux clients du super-marché.
X est le nombre de clients, parmi a et b, qui règlent par chèque , donc X prend les valeur 0,1,2
Y est le nombre de clients, parmi a et b, qui règlent en espèce , donc Y prend les valeur 0,1,2
Tu fais le tableau à double entrée ( par exemple X en ligne et Y en colonne)
Je t'indique le raisonnement de la première ligne
(X,Y)=(0.0) : a et b règlent par carte . Probabilité (0.1)2=0.01(0.1)^2=0.01(0.1)2=0.01
(X,Y)=(1,0) : a OU b règle par chèque et l'autre règle par carte : Probabilité C(2,1)(0.5)(0.1)=0.10C(2,1)(0.5)(0.1)=0.10C(2,1)(0.5)(0.1)=0.10
(X,Y)=(2.0) : a et b règlent par chèque . Probabilité (0.5)2=0.25(0.5)^2=0.25(0.5)2=0.25Tu continues et tu vérifies que la somme des valeurs des lois marginales vaut bien 1.
Je te joins un tableau.
Recompte le car j'ai fait vite.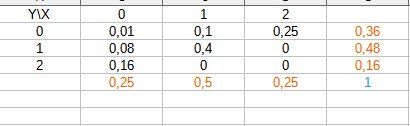
Bons calculs.
-
Lloicstephan dernière édition par loicstephan
@mtschoon a dit dans Loi conjointe du couple probabilité :
X,Y)=(1,0) : a OU b règle par chèque et l'autre règle par carte : Probabilité C(2,1)(0.5)(0.1)=0.10C(2,1)(0.5)(0.1)=0.10C(2,1)(0.5)(0.1)=0.10
bonjour madame
si XXX prend la valeur 111 et 000 pour Y il y a deux possibilite pour Y soit il regle aussi par cheque soit il egle par espece du coup la probabilite conjointe est 0.5×(0.5+0.1)0.5 \times (0.5+0.1)0.5×(0.5+0.1) car si y ne regle pas par espece il peut soit regler par cheque soit regler par cartequ'en pensez vous ou alors j'analyse mal je suis un peu perplexe vis a vis de votre raisonnement notemment pour le couple (1,0)(1,0)(1,0)
-
mtschoon dernière édition par mtschoon

Prends le temps de revois ça de près...
Il ne peut pas y avoir de "+" dans ce calcul (en prenant une combinaison) et ton dénombrement n'est pas bon.
-
Lloicstephan dernière édition par
@mtschoon
okay!
-
mtschoon dernière édition par mtschoon

@loicstephan , je t'explicite le cas (1,0)(1,0)(1,0) si ça t'arrange.
Vu que Y=0, ni a ni b règle en espèce.
Vu que X=1, un règle en chèque et l'autre règle par carte
Tu as deux façons de faire calcul (qui reviennent au même)
1ère méthode :
On choisit une personne parmi les deux qui règle par chèque , et l'autre règlera forcément par carte soit
C21×(0.5)×(0.1)=2×(0.5)×(0.1)=0.01C_2^1\times (0.5)\times (0.1)=2\times (0.5)\times (0.1)=\boxed{0.01}C21×(0.5)×(0.1)=2×(0.5)×(0.1)=0.01
C'est pour cela que je t'ai indiqué qu'il n'y avait pas de "+"C'est ce qui me parait le mieux
2ème méthode si tu souhaites vraiment avoir un "+" : tu sépares les deux cas (au lieu d'utiliser une combinaison) et tu ajoutes.
1ère possibilité : a règle par chèque et b par carte : 0.5×0.10.5\times 0.10.5×0.1
2ème possibilité : a règle par carte et b par chèque : 0.1×0.50.1\times 0.50.1×0.5
TOTAL : (0.5×0.1)+(0.1×0.5)=2×0.5×0.1=0.01(0.5\times 0.1)+(0.1\times 0.5)=2\times 0.5\times 0.1=\boxed{0.01}(0.5×0.1)+(0.1×0.5)=2×0.5×0.1=0.01
-
Lloicstephan dernière édition par
@mtschoon a dit dans Loi conjointe du couple probabilité :
2ème méthode si tu souhaites vraiment avoir un "+" : tu sépares les deux cas (au lieu d'utiliser une combinaison) et tu ajoutes.
1ère possibilité : a règle par chèque et b par carte : 0.5×0.10.5\times 0.10.5×0.1
2ème possibilité : a règle par carte et b par chèque : 0.1×0.50.1\times 0.50.1×0.5
TOTAL : (0.5×0.1)+(0.1×0.5)=2×0.5×0.1=0.01(0.5\times 0.1)+(0.1\times 0.5)=2\times 0.5\times 0.1=\boxed{0.01}(0.5×0.1)+(0.1×0.5)=2×0.5×0.1=0.01elle est olus comprehensible mais alors on prend pas en consideration Y est ce qui le fait que ni a ni b regle en espece siggifi qu'il y a pas de probabilite? en d'autres termes quelle est la probabilite que qucun des deux client ne regle en espece?
-
Lloicstephan dernière édition par loicstephan
@loicstephan
je pense que cette probabilite est de 0.120.1^20.12 qu'est ce que vous en pensez?
-
mtschoon dernière édition par mtschoon

il faut d'abord savoir de quel évènement il s'agit et ensuite (seulement ensuite ) chercher la probabilité correspondante.
Y=0 veut dire que a et b ne règlent pas en espèce, donc ils uilisent forcément carte / chèque.
Comme X=1, un ( un seul ) utilise chèque dont l'autre, par déduction, utilise carte. C'est de la logique .
Ensuite, tu calcules la probabilité correspondante.(0.1)2(0.1)^2(0.1)2 donne effectivement 0.01, mais cela ne reflète pas la démarche à faire.
-
Lloicstephan dernière édition par loicstephan
@mtschoon
ca veut dire qu'a chaque fois que XXX ou YYY prend la valeur 0 on exclu deja ce ces cas la merci
maintenat si XXX ou YYY prend la valeur 1 ou a deux possibilite soit a utiise le moyen de paiement de XXX et bbb ne le fais pas soit bbb le fait et aaa ne le fait pas selon que l'on analyse XXX ou YYY
maintenat losque XXX ou YYY prend la valeur 222 les deux client utilise le moyen de paiment de XXX et vice versa
je crois que ca synthetise un peu dite le moi si j'ai bien compris j'ai ssaie de raissoner comme ca et le compare mes resultats aux votres
-
Lloicstephan dernière édition par
merci bien j'ai tout analyse ca corobore merci je passe aux questions suivantes !
-
Lloicstephan dernière édition par
pour la quesstion suivante les loi marginales sont l'ensemble des valeur de XXX et
je joins mes calculs et je passe a la question suivante!
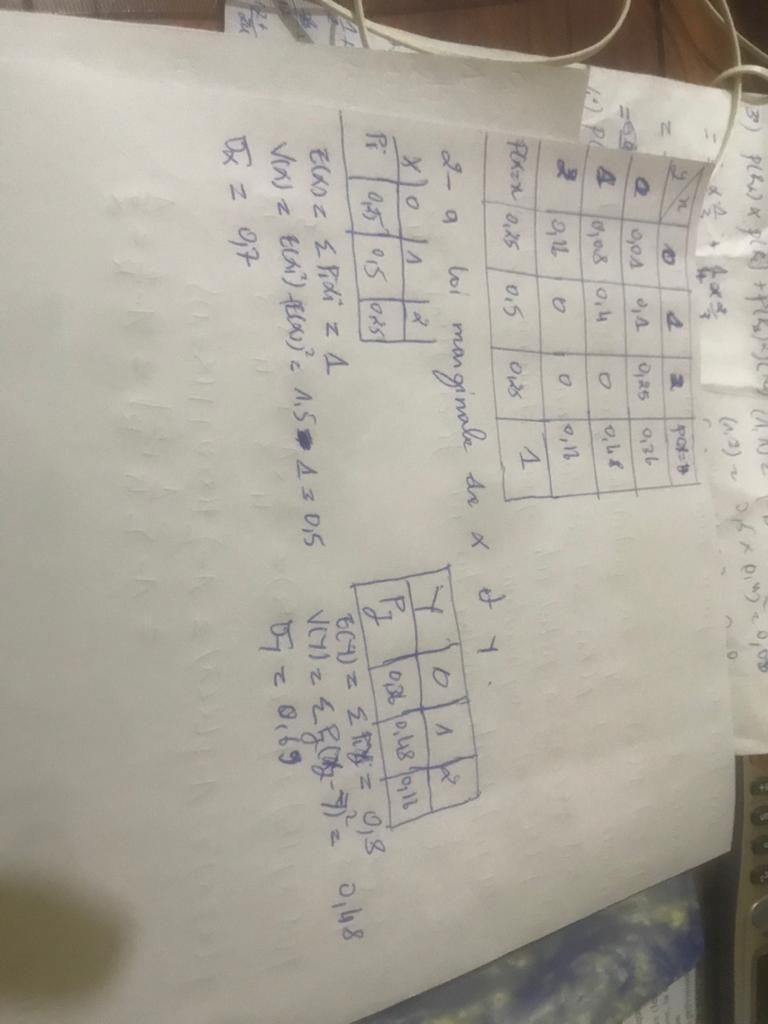
-
mtschoon dernière édition par mtschoon

@loicstephan , bonsoir,
Les lois marginales sont écrites en orangé sur mon tableau et tu peux voir que les deux sommes valent bien 1.
Vérifie si tu trouves pareil.
-
Lloicstephan dernière édition par
je joins la loi de Y/X
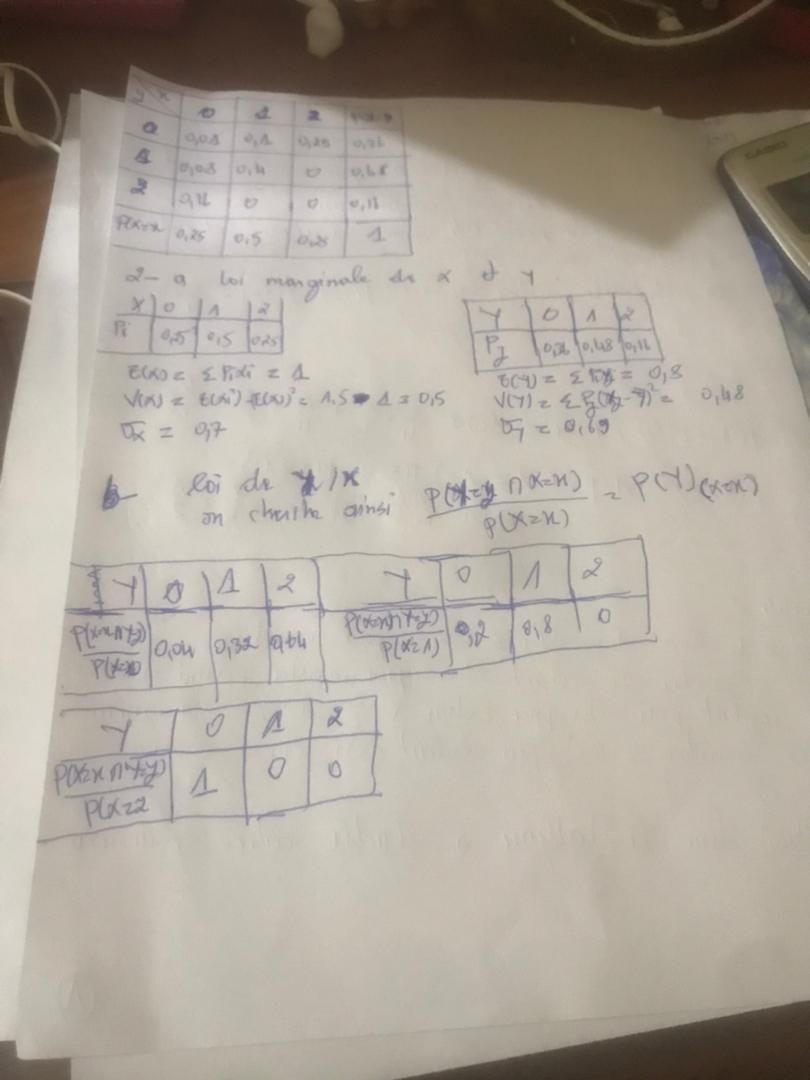
-
Lloicstephan dernière édition par
en ce qui concerne la fonction generatrice bivariee je bloque un peu!
-
mtschoon dernière édition par

@loicstephan , re-bonjour,
IL faudra que tu regardes ton cours de près car je n'ai plus les définitions en tête.
Bon travail.
-
Lloicstephan dernière édition par
bonsoir madame @mtschoon
je joins ici un lien
https://fr.wikiversity.org/wiki/Fonction_génératrice/Fonction_génératrice_d'un_couple_de_variables_aléatoiresje n'ai personellement pas encore fait d'application
donc je continu avec les question suivante sur la correlation et la covariance
-
mtschoon dernière édition par mtschoon

@loicstephan , bonjour,
Pour la covariance, il y a plusieurs formules possibles.
Le plus clair me parait être celle-ci :cov(X,Y)=E(XY)−E(X)E(Y)cov(X,Y)=E(XY)-E(X)E(Y)cov(X,Y)=E(XY)−E(X)E(Y)
Tu as déjà calculé E(X)E(X)E(X) et E(Y)E(Y)E(Y)
E(X)=1E(X)=1E(X)=1 et E(Y)=0.8E(Y)=0.8E(Y)=0.8Il te reste à calculer E(XY)E(XY)E(XY)
Tu utilises le tableau de la loi conjointe.
Pour chaque valeur (xi,yj)(x_i,y_j)(xi,yj) du couple(X,Y), tu calcules le produit xiyjx_iy_jxiyj que tu multiples par la probabilité pi,jp_{i,j}pi,j associée et tu ajoutes.Ici, ça te fait 9 termes à ajouter dont 1 seul n'est pas nul
E(XY)=(1×1)×0.4=0.4E(XY)=(1\times 1) \times 0.4=0.4E(XY)=(1×1)×0.4=0.4
Donc cov(X,Y)=0.4−(1)(0.8)=−0.4cov(X,Y)=0.4-(1)(0.8)=-0.4cov(X,Y)=0.4−(1)(0.8)=−0.4
Le coefficient de corrélation linéaire, noté souvent rrr est :
r=cov(X,Y)σ(X)σ(Y)r=\dfrac{cov(X,Y)}{\sigma(X)\sigma(Y)}r=σ(X)σ(Y)cov(X,Y)
Tu as déjà calculer les deux écarts-type et tu as cov(X,Y)cov(X,Y)cov(X,Y), donc tu peux caluler rrr
Si besoin, tu peux regarder là.
http://renaud.bourles.perso.centrale-marseille.fr/MathsFi/Chap 5 - Couple de variables aleatoires.pdf
-
Lloicstephan dernière édition par
bonsoir merci bien madame !
je suppose qu'a la question 4 on me demande P(Y/X=1)
puis que si x prend la aleur 2 tous les client paient en ccheque donc aucun par carte de meme si X=0 aucun ne paie en cheque donc plus de 1 paeint par carte si oui dite le moi je determine
-
Lloicstephan dernière édition par
de meme pour la fonction generatrice du couple je join cette image
qui donne la formule
-
mtschoon dernière édition par mtschoon

@loicstephan , bonjour,
Je regarde ta proposition pour la question 4
Non, il n'est pas question de X=1, car X représente le nombre de de clients qui règlent par chèque, alors qu'il s'agit dans cette question du nombre de clients qui règlent par carte bancaire
Tu peux prendre une nouvelle variable Z représentant le nombre de clients qui règlent par carte bancaire
Si Z=1, Y prend les valeurs 0 , 1.
La question consiste à chercher deux probabilités conditionnelles :
PZ=1(Y=0)\boxed{P_{Z=1}(Y=0)}PZ=1(Y=0) et PZ=1(Y=1)\boxed{P_{Z=1}(Y=1)}PZ=1(Y=1)
Pour Z=1Z=1Z=1 et Y=0Y=0Y=0, on déduit que X=1X=1X=1
PZ=1(Y=0)=P(X=1)∩(Y=0)P(Z=1)=P((X,Y)=(1,0))P(Z=1)P_{Z=1}(Y=0)=\dfrac{P(X=1)\cap (Y=0)}{P(Z=1)}=\dfrac{P((X,Y)=(1,0))}{P(Z=1)}PZ=1(Y=0)=P(Z=1)P(X=1)∩(Y=0)=P(Z=1)P((X,Y)=(1,0))
Pour Z=1Z=1Z=1 et Y=Y=Y=1, on déduit que X=0X=0X=0
PZ=1(Y=1)=P(X=0)∩(Y=1)P(Z=1)=P((X,Y)=(0,1))P(Z=1)P_{Z=1}(Y=1)=\dfrac{P(X=0)\cap (Y=1)}{P(Z=1)}=\dfrac{P((X,Y)=(0,1))}{P(Z=1)}PZ=1(Y=1)=P(Z=1)P(X=0)∩(Y=1)=P(Z=1)P((X,Y)=(0,1))
Les numérateurs de ces deux probabilités se lisent dans le tableau de la loi conjointe (couleur orange dan mon schéma)
Reste à calculer P(Z=1)P(Z=1)P(Z=1)
Si Z=1Z=1Z=1, (X,Y)=(0,1)(X,Y)=(0,1)(X,Y)=(0,1) ou (X,Y)=(0,1)(X,Y)=(0,1)(X,Y)=(0,1)
Donc,P(Z=1)=P((X,Y)=(0,1))+P((X,Y)=(1,0))P(Z=1)=P((X,Y)=(0,1))+P((X,Y)=(1,0))P(Z=1)=P((X,Y)=(0,1))+P((X,Y)=(1,0))
Le dénominateur de ces deux probabilités se calcule en ajoutant deux valeurs du tableau de la loi conjointe (couleur orange dan mon schéma)
Bons calculs.