Utilisation du triangle de Pascal

Bonsoir chers tous.
Je dois montrer que $C_{p+1}^{n+1}$ + $C_{p+1}^{n}$ = $C_{p+2}^{n+1}$
Dans mon exercice, ils disent avoir utilisé le triangle de Pascal pour démontrer cela.
J'aimerais donc comprendre comment faire cela avec le triangle de Pascal.
Ps1 : Je ne connait pas grand-chose dans cette méthode.
Ps2: Pour les combinaisons ci-dessus, la notation utilisée est celle qui ressemble aux matrices. Vu que je ne sais pas les faire avec du LaTex, j'ai opté pour cette notation.

@Wil-Fried , c'est la formule de Pascal que tu veux démontrer.

Regarde ici , si besoin (il faudra que tu changes les notations):
http://www.jybaudot.fr/Probas/democombi.html

C'est effectivement la méthode que l'on utilise pour construire le Triangle de Pascal, mais de dirais que c'est grâce à cette formule que l'on peut justifier le triangle de Pascal.

Tu peux voir le lien direct entre la formule et le triangle ici (et il y a aussi une démonstration de la formule)
https://www.youtube.com/watch?v=JwMXMl3oaa0

@Wil-Fried , bonjour,

Si ça t'interesse, Je t'indique l'écriture en latex pour obtenir $(nk){n}\choose{k}$ :

Tu tapes, sans espaces $ {n}\choose{k} $

@Wil-Fried , j'espère qu'avec la video sur le triangle de Pascal, tu as compris le principe.

Les notations que tu indiques sont un peu bizarres...

Il faut donc que tu justifies que :

$(np+1){n}\choose{p+1}$ + $(np+2){n}\choose{p+2}$ = $(n+1p+2){n+1}\choose{p+2}$

Je te mets un schéma correspondant à tes notations, pour indiquer le mécanisme de triangle de Pascal pour le calcul des coefficients binomiaux (combinaisons) :

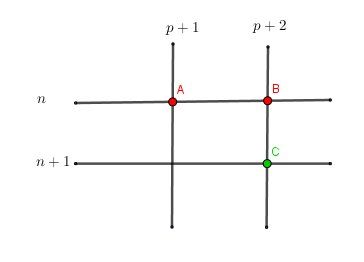
Il y a la colonne $(p + 1)$ et la colonne $(p + 2)$
Il y a la ligne $n$ et la ligne $n + 1$

Les points d'intersection utiles sont $A, B, C$

$A$ (en rouge) représente $(np+1){n}\choose{p+1}$
$B$ (en rouge) représente $(np+2){n}\choose{p+2}$
$C$ (en vert ) représente $(n+1p+2){n+1}\choose{p+2}$

Connaisant les valeurs de A et B, on obtient la valeur de C avec la formule $A+B=C\boxed{A+B=C}$ c'est à dire ici : $(np+1){n}\choose{p+1}$ + $(np+2){n}\choose{p+2}$ = $(n+1p+2){n+1}\choose{p+2}$
(c'est la formule de Pascal)

Le triangle de Pascal permet ainsi de calculer, de proche en proche, les coefficients binomiaux par de simples additions.

C'est peut-être seulement cela qui est à indiquer dans ton exercice, mais ce n'est pas une "démonstration" , c'est l'utilisation de la formule de Pascal appliquée au triangle de Pascal.

Bon travail .

@mtschoon Merci beaucoup. A vrai dire, au départ j'avais pas compris, mais avec cette démonstration à l'appuie, ça vaut bien maintenant.

@mtschoon On me demande d'en déduire le calcul de :
$∑k=0nk(k+1)(k+2)...(k+i−1)\sum_{k=0}^{n}k(k+1)(k+2)...(k+i-1)$
Je suis perdu à ce niveau!
Une idée que j'ai est de transformer cette somme de sorte à avoir un truc similaire à la formule démontrée à la première question. Mais je ne sais pas comment faire cela.

@Wil-Fried , bonjour,

Je reste perplexe devant ta formule car je me demande bien ce que vaut $i$ ...

@mtschoon Voilà!! C'est pourtant ce que l'exercice me demande. Je me posais donc la même question que vous, quel est le rôle de $i$ ici ?

J'ai essayé plus ou moins d'interroger Google et j'ai vu une publication d'un autre étudiant qui posait la même préoccupation. Mais dans son énoncé à lui c'était un $p$ à la place du $i$ . Boff je me dis que c'est la même chose.

Par ailleurs, lorsque j'ai trouvé un élément de correction, il à été dit la dedans que $k(k+1)(k+2)...(k+i−1)=(k+i−1)!(k−1)!k(k+1)(k+2)...(k+i-1)=\frac{(k+i-1)!}{(k-1)!}$ = $i!(k+i−1)!i!(k−1)!=i!\frac{(k+i-1)!}{i!(k-1)!}=$ i!$ $(k+1−ik){k+1-i}\choose{k}$

Mais à vrai dire je ne comprends pas cette démonstration.

Bonsoir,

Désolée, mais ton énoncé ne me parait pas fiable...!
Tu peux peut-être essayer d'avoir des informations.
Je ne peux pas dire plus.

@mtschoon C'est compris. Merci beaucoup.