Exercice : Calcul intégral

Bonsoir, svp aidez moi à démontrer ceci :

Vérifier que pour tout p tel que 2<=p<=n-1,
(1/n)log(p/n) est compris entre :

A gauche de l'inégalité on a
Intégrale allant de (p-1)/n à p/n de log(x)dx
A droite de l'inégalité on a :
Intégrale allant de p/n à (p+1)/n de log(x)dx

Les inégalités ne sont pas strictes.

Il s'agit de la comparaison aire et intégrale.
Avec un schéma, tu dois y arriver.
Si besoin, je te ferai un schéma .

Remarque ( qui ne change pas la question) :
Dans ton énoncé, $l o g$ représente la fonction logarithme décimal ou logarithme népérien (qui se note habituellement $l n$ )?

@mtschoon a dit dans Exercice : Calcul intégral :

@Wil-Fried , bonjour,

Il s'agit de la comparaison aire et intégrale.
Avec un schéma, tu dois y arriver.
Si besoin, je te ferai un schéma .

Remarque ( qui ne change pas la question) :
Dans ton énoncé, $l o g$ représente la fonction logarithme décimal ou logarithme népérien (qui se note habituellement $l n$ )?

Bonjour,

C'est bien dans le mot "habituellement" que le bât blesse.

Petite histoire de ce logarithme naturel (de wiki)

Cette fonction fut notée l. ou l, dès le début du XVIIIe siècle1, et jusque dans la première moitié du XIXe siècle2, puis log. ou log dès la fin du XVIIIe siècle, puis Log pour la différencier de la fonction log (logarithme de base quelconque, ou plus particulièrement logarithme décimal), ou encore logh (« logarithme hyperbolique »)6, avant que ne tente de s'imposer la notation préconisée par les normes AFNOR de 19617 et ISO 80000-28 : la notation ln. Avec un succès cependant très relatif : la notation log est encore aujourd'hui utilisée dans plusieurs branches des mathématiques, et tout particulièrement en théorie des nombres, ainsi que dans plusieurs langages de programmation, comme C, C++, SAS, R, MATLAB, Mathematica, Fortran, et BASIC.

Pourquoi faire simple ... quand on peut faire compliqué.

Bonjour,

@Wil-Fried , je te joins un schéma (pour comprendre l'idée)

La fonction logarithme que tu appelles ' $l o g$ ' (que ça soit log décimal ou log népérien) est strictement croissante.
Dans le schéma que je te joins, elle est en rouge.
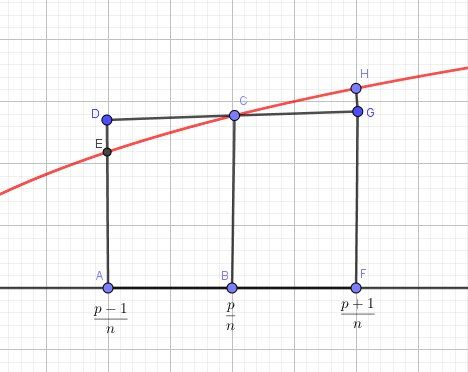
intégrale.jpg

$1nlog(pn)\dfrac{1}{n}log(\dfrac{p}{n})$ représente l'aire du rectangle $A B C D$ et aussi l'aire du rectangle $B F G C$

$∫p−1npnlog(x)dx\displaystyle \int_{\dfrac{p-1}{n}}^{\dfrac{p}{n}}log(x)dx$ représente l'aire du quadrilatère curviligne $A B C E$

$∫pnp+1nlog(x)dx\displaystyle \int_{\dfrac{p}{n}}^{\dfrac{p+1}{n}}log(x)dx$ représente l'aire du quadrilatère curviligne $B F H C$

Tire la conclusion souhaitée.

Reposte si besoin.

@mtschoon Bonjour. Mon exercice n'a pas donné de spécification précise sur la nature de log. Heureusement que cela ne change rien à la question.

@mtschoon svp, je n'ai pas vraiment compris l'explication avec le schéma. Aussi, je crois que je dois répondre à la question analytiquement, du coup avec le schéma je ne sais pas trop comment m'y prendre.

Oui @Wil-Fried , l'intérêt est que la fonction soit croissante (strictement croissante n'est même pas obligatoire vu que tu indiques que les inégalités ne sont pas strictes).

Regarde si besoin ton cours sur aire et intégrale
(aire comprise entre la courbe et l'axe des abscisses)

L'aire d'un rectangle est le produit de la largeur par la longueur
Les deux rectangles ont pour "largeur" $1n\dfrac{1}{n}$
car
$pn−p−1n=1n\dfrac{p}{n}-\dfrac{p-1}{n}=\dfrac{1}{n}$
et
$p+1n−pn=1n\dfrac{p+1}{n}-\dfrac{p}{n}=\dfrac{1}{n}$

Les deux rectangles ont pour "longueur" $pn\dfrac{p}{n}$

Evidemment, tu ne peux pas répondre seulement avec un schéma, mais peux faire le schéma qui illustre la démarche et écrire les inégalités correspondantes, à condition que tu aies compris le schéma...

Bonjour,

Attention quant même, si on essaie de démontrer en calculant les intégrales et ...

Avec les conditions imposées 2 <= p <= n-1, on a toujours 0 < (p/n) < 1 et donc (1/n).ln(p/n) est < 0

Et donc attention aux comparaisons entre des valeurs négatives ...
Ce n'est pas un gros problème, mais nécessite de faire attention.

Avec par exemple p = 5 et n = 10

1/n*ln(p/n) = -0,0693...

$∫p−1npnln(x)dx=∫410510ln(x)dx=−0,080...\int_{\frac{p-1}{n}}^{\frac{p}{n}}ln(x) dx = \int_{\frac{4}{10}}^{\frac{5}{10}}ln(x) dx = -0,080...$

$∫pnp+1nln(x)dx=∫510610ln(x)dx=−0,0599...\int_{\frac{p}{n}}^{\frac{p+1}{n}}ln(x) dx = \int_{\frac{5}{10}}^{\frac{6}{10}}ln(x) dx = -0,0599...$

@mtschoon merci beaucoup

@Wil-Fried ,comme te le dit @Black_Jack, en respectant les conditions de l'énoncé, tu travailles sur l'intervalle [0,1], et la fonction dont il s'agit, si c'est bien une fonction logarithme, prends des valeurs négatives sur cet intervalle.

Toutes les ordonnées utilisées sont négatives ; les aires considérées sont des aires algébriques négatives (regarde ton cours).

Je te joins le schéma , avec les mêmes notations, mais dans la zone $∈[0,1]\in [0,1]$ .
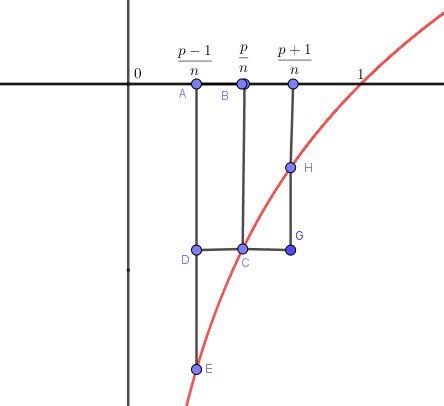
intégraleBis.jpg

Bon courage !