3. Groupes : sous-groupe engendré

Groupes : sous-groupe engendré

  • O

    Bonsoir, Voici la question suivante :
    " Soit H un sous-groupe strict d'un sous groupe ( G ; * ). Déterminer le sous groupe engendré par le complémentaire".

    On m'a introduit les sous-groupes engendré par un élément "a" comme le plus petit sous-groupe contenant l'élément "a".

    Dans la correction, il suppose dès le début que le groupe engendré est G lui-même.
    Mais je ne comprends pas pourquoi cela ne peut pas être K (le complémentaire de H ) union l'élément neutre de G.
    En effet, comme G est un groupe, donc tous ces éléments sont inversibles.
    On sait que H est un sous-groupe de G, donc il contient l'élément neutre de G et tous ses éléments possèdent un inverse. Comme H et K sont disjoints, pour que G soit un groupe, il faut forcément que les éléments de K possède leur inverse car ces inverses ne peut être dans H, ils sont donc forcément dans K. Il manque donc à K l'élément neutre de G pour être un sous-groupe.
    Donc K U {e} est bien le plus petit sous-groupe contenant K, non ?

    Merci d'avance pour vos retours.

  • mtschoon

    Bonjour @OKiDoK ,

    Je répondrais NON à ta proposition ; tu ne peux pas affirmer que K∪K \cup K∪ {e} est un sous groupe.

    Ce que tu indiques est juste mais incomplet.
    Il faudrait, en plus, que K∪K \cup K∪ {e} soit stable pour la loi * , et on n'en sait rien...

    Un contre-exemple simple.

    Soit ZZZ muni de la loi + : c'est un groupe.

    Soit HHH l'ensemble des entiers pairs ( muni de la loi +) :
    On prouve facilement que HHH est un sous groupe strict de ZZZ (l'élément neutre est 000 et le symétrique de chaque élément est l'opposé de l'élément)

    Soit KKK le complémentaire de HHH : c'est l'ensemble des entiers impairs.
    K∪K \cupK∪ {0} est-il un sous groupe ? NON

    Pas de problème relatif aux symétriques :
    le symétrique de (2n+1)est (-2n-1) et
    (2n+1)+(-2n-1)=(-2n-1)+(2n+1)=0

    Par contre, K∪K\cupK∪ {0} n'est pas stable pour la loi +
    par exemple :
    −3-3−3 et 555 sont dans K∪K\cupK∪ {0}
    (−3)+5=2(-3)+5=2(−3)+5=2 ; 222 est pair , il n'appartient pas à K∪K\cupK∪ {0}

  • mtschoon

    @OKiDoK

    Effectivement, c'est surprenant qu'il soit indiqué, sans preuve, que le sous-groupe engendré soit GGG lui-même.
    Deux possibilités :
    Soit cela fait partie de ton cours, donc tu peux l'utiliser directement.
    Soit cela a été démontré dans une question précédente.

    Si besoin, je te donne quelques pistes de démonstration.
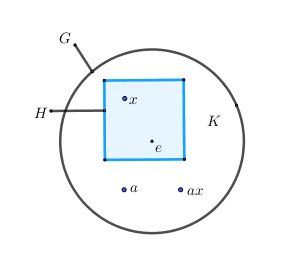
    groupe.jpg

    Soit aaa un élément fixé de KKK
    On cherche le sous groupe engendré par KKK nommé EEE
    Nécessairement K⊂E\boxed{K\subset E}K⊂E​

    Soit xxx un élément quelconque de HHH
    On peut prouver que ax∉Hax\notin Hax∈/​H
    En effet, si ax∈Hax\in Hax∈H, vu que x−1∈Hx^{-1}\in Hx−1∈H , on déduit que axx−1∈Haxx^{-1}\in Haxx−1∈H c'est à dire que a∈Ha\in Ha∈H donc Contradiction
    donc ax∈Kax\in Kax∈K

    Bilan :
    {ax∈Ka∈K\begin{cases}ax\in K\cr a\in K \end{cases}{ax∈Ka∈K​ donc {ax∈Ea∈E\begin{cases}ax\in E\cr a\in E \end{cases}{ax∈Ea∈E​
    Vu que EEE est un sous-groupe, a−1∈Ea^{-1}\in Ea−1∈E, donc a−1ax∈Ea^{-1}ax\in Ea−1ax∈E donc x∈Ex\in Ex∈E

    Conclusion : Tout élément xxx de HHH appartient à EEE donc, H⊂E\boxed{H\subset E}H⊂E​
    EEE contient à la fois KKK et HHH donc E=G\boxed{E=G}E=G​

    Bonne lecture.

  • O

    Je vous remercie pour vos retours simples, clairs et complets !

  • mtschoon

    De rien @OKiDoK
    Si tout est OK pour toi, c'est parfait.

  • O

    Re-Bonjour, désolé de vous déranger à nouveau, j'ai une nouvelle question en rapport avec cette exercice.
    Si on pose K = { t ; t^-1 }. Comment peut-on résoudre la question en démontrant que par itération de la loi *, sur l'élément t et son inverse, on va pouvoir engendré tous les éléments de H ?

  • mtschoon

    @OKiDoK , re-bonjour,

    Utilise la question précédente et la définition/théorème du sous-groupe engendré par une partie d'un groupe (voir d'un élément d'un groupe).

    Piste à expliciter,

    KKK={t,t−1t,t^{-1}t,t−1}

    Le sous groupe engendré par KKK est GGG.
    Donc, le sous groupe engendré par {t,t−1t,t^{-1}t,t−1} est GGG

    Ton cours doit t'indiquer que le sous groupe engendré par une partie KKK d'un groupe, noté traditionnellement Gr(K)Gr(K)Gr(K) , (ici GGG), est formé par les composés d'un nombre fini d'éléments de KKK et de leurs inverses.

    Ici, les éléments de G sont donc de la forme tαt^\alphatα avec α∈Z\alpha \in Zα∈Z

    En conséquence, les éléments de HHH sont de la forme tαt^\alphatα avec α∈Z\alpha \in Z α∈Z \ {1,−11,-11,−1}

    d'où la réponse.

  • O

    Merci pour votre retour

  • mtschoon

    De rien @OKiDoK et bon travail.

Se connecter pour répondre