Pile ou Face : probabilité d'obtenir 2 piles consécutifs dans une série de n lancers

Bonjour
Je poste ici un peu au hasard non pas qu'il ne s'agisse pas de mathématiques mais une autre rubrique est peut être plus adaptée. Si ce devait être le cas je m'en excuse par avance mais je ne sais pas à quel niveau correspond ma demande.

Pour info j'ai quitté le lycée en 2nde voila 35 ans et je n'étais pas spécialement féru de mathématiques...

Aujourd'hui je cherche une formule qui me permettrait de calculer la probabilité d'obtenir 2 piles consécutifs dans une série de n lancers.

J'ai fait un petit programme qui m'a permis, à l'aide de boucles imbriquées, de déterminer que pour 12 lancers la probabilité d'avoir 2 piles consécutifs est de 90.79...% ( 3179 sur 4096 cas possibles ) mais j'imagine qu'il existe une formule pour calculer cela car mon truc fait vraiment usine à gaz et n'est pas spécialement pratique d'autant que je voudrais aussi tester, par exemple, 3 piles consécutifs su 50 lancers...

Merci pour votre aide

@Stéphane-Perrot , bonsoir,

Je regarde un peu ta question.
La modération la déplacera certainement car elle ne fait pas partie du domaine de la physique.

Ton énoncé manque de précision.
Je suppose que tu parles d'une pièce mais il y a -t-il équiprobabilité entre P (pour pile) et F( pour face)?
Comme tu ne l'indiques pas, j'admet que c'est oui
(1/2 pour chaque probabilité)
Tu ne précises pas s'il s'agit d'avoir exactement 2 piles consécutifs (PP) ou au moins 2 piles consécutifs PP) sur n lancers.
Vu la réponse que tu indiques, j'admet qu'il s'agit d'au moins 2 piles consécutifs.
Tu penses qu'il existe une formule ...Pour avoir cette formule, comme tu dis, il faut la chercher et la trouver (avec un peu d'inspiration et beaucoup de transpiration...)

Je te mets les grandes lignes utilisées pour la trouver, mais ce n'est pas de niveau Seconde...c'est plutôt de niveau Première pour l'arbre, Supérieur pour la suite ...

Idée : passer par l'évènement contraire.
Soit $a_n$ la probabilité de ne pas trouver deux PP consécutifs sur n lancers
La probabilité que tu cherches sera donc $bn=1−an\boxed{b_n=1-a_n}$

Il faut faire des conjectures en utilisant les premiers cas.
Je te joins un arbre probabiliste avec 4 niveaux de branches

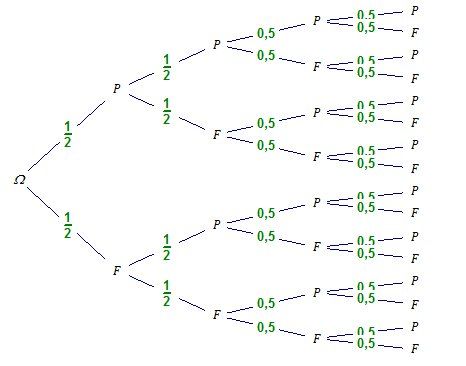
En parcourant l'arbre tu peux trouver $a_1, a_2,a_3,a_4$
tu obtiens :
$a_1=1$
$a2=3(12)2=34a_2=3(\dfrac{1}{2})^2=\dfrac{3}{4}$
$a3=5(12)3=58a_3=5(\dfrac{1}{2})^3=\dfrac{5}{8}$
$a4=8(12)4=816a_4=8(\dfrac{1}{2})^4=\dfrac{8}{16}$
Tu peux compléter, par logique, avec $a_0=1$

Conjectures
$a2=12a1+14a0a_2=\dfrac{1}{2}a_1+\dfrac{1}{4}a_0$
$a3=12a2+14a1a_3=\dfrac{1}{2}a_2+\dfrac{1}{4}a_1$
$a4=12a3+14a2a_4=\dfrac{1}{2}a_3+\dfrac{1}{4}a_2$

On conjecture que pour tout $n$ de $N$ ,
$an+2=12an+1+14an\boxed{a_{n+2}=\dfrac{1}{2}a_{n+1}+\dfrac{1}{4}a_n}$

On doit ensuite faire une récurrence pour preuve générale.

On a donc :
$a_0=1$
$a_1=1$
$an+2=12an+1+14ana_{n+2}=\dfrac{1}{2}a_{n+1}+\dfrac{1}{4}a_{n}$

Il s'agit d'une suite récurrente linéaire d'ordre 2

Equation caratéristique : $r2−12r−14=0r^2-\dfrac{1}{2}r-\dfrac{1}{4}=0$

Solutions : $r1=1+54r_1=\dfrac{1+\sqrt 5}{4}$ et $r2=1−54r_2=\dfrac{1-\sqrt 5}{4}$

Il existe deux réel $α\alpha$ et $β\beta$ tels que
$an=α(1+54)n+β(1−54)na_n=\alpha\biggr(\dfrac{1+\sqrt 5}{4}\biggr)^n+\beta\biggr(\dfrac{1-\sqrt 5}{4}\biggr)^n$

Reste à trouver $α\alpha$ et $β\beta$

En prenant $n = 0$ et $n = 1$ , on obtient le système à résoudre
${a0=α+βa1=α(1+54)+β(1−54)\begin{cases}a_0=\alpha+\beta\cr a_1=\alpha(\dfrac{1+\sqrt 5}{4})+\beta(\dfrac{1-\sqrt 5}{4})\end{cases}$
c'est à dire :
${1=α+β1=α(1+54)+β(1−54)\begin{cases}1=\alpha+\beta\cr 1=\alpha(\dfrac{1+\sqrt 5}{4})+\beta(\dfrac{1-\sqrt 5}{4})\end{cases}$

Après calculs, on obtient :
$α=5+3510\alpha=\dfrac{5+3\sqrt 5}{10}$

$β=5−3510\beta=\dfrac{5-3\sqrt 5}{10}$

La formule finale pour $a_n$ est donc:

$an=(5+3510)(1+54)n+(5−3510)(1−54)n\boxed{a_n=\biggr(\dfrac{5+3\sqrt 5}{10}\biggr)\biggr(\dfrac{1+\sqrt 5}{4}\biggr)^n+\biggr(\dfrac{5-3\sqrt 5}{10}\biggr)\biggr(\dfrac{1-\sqrt 5}{4}\biggr)^n}$

D'où la formule que tu cherches :
$bn=1−(5+3510)(1+54)n−(5−3510)(1−54)n\boxed{b_n=1-\biggr(\dfrac{5+3\sqrt 5}{10}\biggr)\biggr(\dfrac{1+\sqrt 5}{4}\biggr)^n-\biggr(\dfrac{5-3\sqrt 5}{10}\biggr)\biggr(\dfrac{1-\sqrt 5}{4}\biggr)^n}$

Si tu l'appliques à $n = 12$ , tu obtiens :

$a12=3774096a_{12}=\dfrac{377}{4096}$

$b12=37194096b_{12}=\dfrac{3719}{4096}$

(Tu as dû faire une faute de frappe car tu as écrit $3179$ au lieu de $3719$ )

Bonne lecture (et cherche les documents sur le web pour les notions mathématiques utilisées).

Bonsoir,

Merci à la modération d'avoir déplacer ce topic.
Il est maintenant la rubrique "Terminale".
Les "suites récurrentes linéaires d'ordre 2" ne sont vraiment pas au programme de Terminale...elles s'étudient en Sup.

Je me demande s'il ne serait pas mieux dans la rubrique "Supérieur" ou éventuellement dans "Enigmes et curiosités" car le demandeur est de niveau Seconde. Pour lui, ce doit être une curiosité...*

A voir.

Bonsoir,

Merci à la modération pour ce nouveau déplacement.

La demande étant très particulière, cette rubrique où ce topic est maintenant, conviendra je pense.