3. la derivabilite de la partie entiere

la derivabilite de la partie entiere

  • M

    f(x) = x|x|(x − E(x)) , aidez moi a etudier la derivabilite de cette fonction

  • mtschoon

    @MERIEM , bonjour,

    Si c'est la dérivabilité de cette fonction sur RRR , il y a du travail (car différents cas à considérer)

    Si tu veux d'abord te faire une idée de cette fonction , je te mets une représentation graphique ( tu peux l'obtenir sur ta calculette)
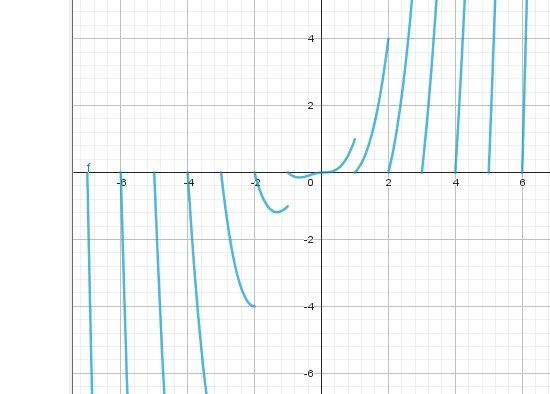
    floorX.jpg

  • mtschoon

    Je te conseille de voir séparément les cas x non entier et le cas x entier

    Quelques pîstes de travail,

    1er cas : x∈]n,n+1[x\in ]n,n+1[x∈]n,n+1[ avec n entier positif (n=0,1,2,3,...n=0,1,2,3,...n=0,1,2,3,...)

    x>0x \gt 0x>0 donc ∣x∣=x|x|=x∣x∣=x
    n<x<(n+1)n\lt x\lt(n+1)n<x<(n+1) donc E(x)=nE(x)=nE(x)=n
    f(x)=x2(x−n)=x3−nx2f(x)=x^2(x-n)=x^3-nx^2f(x)=x2(x−n)=x3−nx2
    f est un polynome du 3ème degré donc dérivable
    f′(x)=3x2−2nxf'(x)=3x^2-2nxf′(x)=3x2−2nx

    2ème cas : x∈]n,n+1[x\in ]n,n+1[x∈]n,n+1[ avec n entier négatif (n=−1,−2,−3,...)(n=-1,-2,-3,...)(n=−1,−2,−3,...)
    x<0x \lt 0x<0 donc ∣x∣=−x|x|=-x∣x∣=−x
    n<x<(n+1)n\lt x\lt(n+1)n<x<(n+1) donc E(x)=nE(x)=nE(x)=n
    Tu traites ce cas comme le premier cas.
    f dérivable

    3ème cas : x=0x=0x=0
    Tu peux étudier la dérivée (à gauche et à droite) avec la définition de dénombre dérivé

    f(0)=0f(0)=0f(0)=0
    Pour x∈]0,1[,E(x)=0x\in]0,1[, E(x)=0x∈]0,1[,E(x)=0 f(x)=x3f(x)=x^3f(x)=x3
    lim⁡x→0,x>0f(x)−f(0)x−0=lim⁡x→0,x>0x2=0\displaystyle \lim_{x\to 0, x\gt 0}\dfrac{f(x)-f(0)}{x-0}=\lim_{x\to 0, x\gt 0}x^2=0x→0,x>0lim​x−0f(x)−f(0)​=x→0,x>0lim​x2=0
    f dérivable à droite en 000 ( le nombre dérivé à droite vaut 0)

    Tu traites de même la dérivabilité à gauche en 0
    Pour x∈]−1,0[,E(x)=−1x\in]-1,0[, E(x)=-1x∈]−1,0[,E(x)=−1 et ∣x∣=−x|x|=-x∣x∣=−x
    Tu dois trouver que f est dérivable à gauche en 000 ( le nombre dérivé à gauche vaut 0)

    Au final, f est dérivable en 0 et f′(0)=0f'(0)=0f′(0)=0

    4ème cas : x entier non nul
    Tu peux raisonner comme pour le 3ème cas et tu trouveras f dérivable à droite mais pas à gauche,
    donc f non dérivable.

    Remarque : pour le 4ème cas, si tu connais , tu pourrais passer par la non-continuité (ce qui serait plus rapide peut-être)
    Par théorème :
    si une fonction est dérivable en un point , elle est continue en ce point
    si elle n'est pas continue en un point, elle n'est pas dérivable en ce point.
    Donc , dans le 4ème cas, tu peux prouver que la fonction n'est pas continue donc pas dérivable.

    Bon travail !

Se connecter pour répondre