Domaine de définition d'une fonction à deux variables
-
FFan-maths dernière édition par Noemi
Bonjour,
j'ai une fonction à deux variables dont je dois déterminer le domaine de définition.
La voici : f(x,y)=xy−x+2y−2f(x,y)=\sqrt{xy-x+2y-2}f(x,y)=xy−x+2y−2
Je vous poste aussi ma proposition dont j'ai un doute :

Mon doute porte sur la distinction des deux intervalles de y.
Merci à vous de votre aide,
Cordialement,
-
mtschoon dernière édition par mtschoon

@Fan-maths , bonsoir,
Ton idée me semble bonne.
Tu aurais aussi pu factoriser:
x(y−1)+2(y−1)≥0x(y-1)+2(y-1)\ge 0x(y−1)+2(y−1)≥0 c'est à dire
(x+2)(y−1)≥0(x+2)(y-1)\ge 0(x+2)(y−1)≥0Produit positif c'est à dire deux facteurs de même signe,
ce qui donne :
(x+2)≥0(x+2)\ge 0(x+2)≥0 et (y−1)≥0(y-1)\ge 0(y−1)≥0
ou
(x+2)≤0(x+2)\le 0(x+2)≤0 et (y−1)≤0(y-1)\le 0(y−1)≤0c'est à dire
x≥−2 et y≥1\boxed{x\ge -2\ et \ y\ge 1}x≥−2 et y≥1 (quart de plan en bleu)
ou
x≤−2 et y≤1\boxed{x\le -2\ et \ y\le 1}x≤−2 et y≤1 (quart de plan en rose)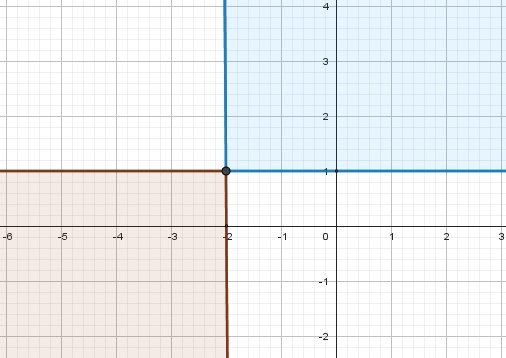
-
FFan-maths dernière édition par
Bonjour,
OK, merci beaucoup pour votre méthode. Elle me parait plus "propre" que la mienne.
Bien cordialement,
-
mtschoon dernière édition par

De rien @Fan-maths !
Effectivement, quand on peut éviter des divisions (qui nécessitent des conditions), ça évite les complications..