PETIT EXERCICE PROBABILITES [ Besoin d'aide ]

[Robz]

Bonjour je ne comprends cette exercice, quelqu'un aurait t'il la gentillesse de m'aider, en vous remerciant.

Le Père Noël se déplace aléatoirement entre trois villes A, B et C selon le protocole suivant :

-A l'instant 0, le Père Noël se trouve en A.**
-Lorsque le Père Noel est à un instant donné dans une ville, à l'instant suivant : soit il y reste avec une probabilité de j, soit il se déplace dans une des deux autres villes avec la même probabilité pour chacune de ces deux villes.

On ne considère que les instants entiers : 0,1,2, ..., et on néglige les temps de trajet entre deux villes.

On definit pour tout n E N, les événements An, Bn, Un par :

An : « le Père Noël est en A à l'instant n »,
Bn: « le Père Noël est en B à l'instant n »,
Cn : « le Père Noel est en C à l'instant n ».

On pose an = P(An), bn = P(Bn) et Cn = P(Cn)

1. Préciser la valeur de a0, d0, et c0.
   2)Montrer que pour tout n E N, (An, Bn, Cn) est un système complet d'événements.
   3)Quelle est la valeur de An + Bn + Cn , pour n E N ?

[mtschoon]

@Robz , bonjour,

Je regarde un peu ton exercice.

Pour le 1 ),

$a_0=1,b_0=0,c_0=0$ vu que le Père Noêl est dans la ville A (et pas dans les deux autres)

Pour le 2 ),

Soit E={$A_n,B_n,C_n$}

Dans E, il y a un et un seul évènement réalisé, vu que le Père Noël est forcément dans une de ces villes mais pas dans les trois à la fois.

Tu peux donc appliquer la définition de système complet d'évènements.
Voir la définition ici (Système exhaustif)
https://fr.wikipedia.org/wiki/Système_exhaustif

Pour la 3 ), je pense que tu as voulu écrire $a_n+b_n+c_n$ car on ajoute des probabilités , pas des évènements.

$a_n+b_n+c_n=1$

C'est à peu près évident.
Pour le prouver, une récurrence convient très bien.

Reposte si besoin.

[Robz]

@mtschoon Merci beaucoup de ton aide, c'est gentil, dernière question, pour la récurrence et particulièrement pour l'hérédité, comment faire ? En te remerciant.

[mtschoon]

@Robz , idées pour la récurrence,

Pour l'initialisation, il suffit d'indiquer que $a_0+b_0+c_0=1$ , vu la réponse à la 1 )

Pour l'hérédité,
Hypothèse à un ordre $n$ de $N$ : $a_n+b_n+c_n=1$
Conclusion à démontrer : $a_{n+1}+b_{n+1}+c_{n+1}=1$

Piste pour la démonstration,
Je te mets une portion d'arbre probabiliste pour passer de l'état $n$ à l'état $(n+1)$

$j$ est la probabilité lorsque le Père Noël reste dans une ville et $k$ la probabilité lorsqu'il se déplace dans une autre ville.
Donc, $j+k+k=1$ <=> $j+2k=1$ <=> $k=\frac{1-j}{2}$

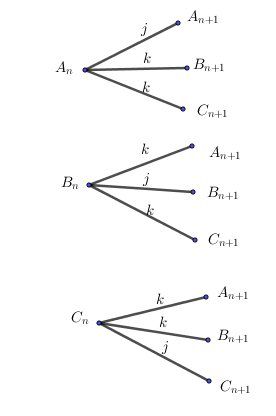
Avec l'arbre, tu obtiens:
$a_{n+1}=a_{n}j+b_{n}k+c_{n}k$
$b_{n+1}=a_{n}k+b_{n}j+c_{n}k$
$c_{n+1}=a_{n}k+b_{n}k+c_{n}j$

Tu fais la somme $a_{n+1}+b_{n+1}+c_{n+1}$
Tu dois trouver , après calculs et factorisation,
$a_{n+1}+b_{n+1}+c_{n+1}=(a_n+b_n+c_n)(j+2k)=1\times 1=1$

Bons calculs.