Calcul de développement limité

[Wil Fried]

Bonsoir, besoin d'aide svp.
J'ai la fonction f définie par raccordement de la façon suivante :
Lorsque x # 0, f(x) vaut (1/e)[(1+x)^((x+2)/2x)]
Et lorsque x=0, f(x) vaut 1.

1. Donner le Dl à l'ordre 2 de la fonction ln(1+x) au voisinage de 0.
   J'ai trouvé comme Dl : x-(1/2)x^2 + o(x^2)
   Mais dans la correction ils sont allés à l'ordre 3, Je ne comprend pas pourquoi.

2. Donner le Dl à l'ordre 1 de f au voisinage de 0. Montrer que f est continue et dérivable en 0.
   Je suis passé par le logarithme de la fonction f, et je trouve que son logarithme a un Dl au voisinage de 0 à l'ordre 2 égal à -×^2/4. Ensuite, je prend donc l'exponentiel de ce résultat. D'où je cherche le Dl au voisinage de 0 du résultat. Je trouve ainsi, au regard du Dl de l'exponentiel, 1-(x^2)/4.
   Mais dans la correction, ils trouvent comme resultat 1-(x^2)/12. Je ne sais comprend pas pourquoi.

Et pour finir, je ne sais pas comment montrer que la fonction est continue et dérivable en 0.
Merci d'avance pour votre aide.

[Black-Jack]

Bonjour,

Je ne suis pas matheux ... mais ce que je sais est qu'il y a rarement une manière unanime des matheux d'interprétation sur presque toutes les " conventions".

Pour le DL à l'ordre 2 au voisinage de 0 de ln(1+x) il y a 2 écoles (chacune pensant évidemment avoir raison).

La première approche travaille directement à partir de la fonction ln(1+x) ...
et aboutit au DL à l'ordre 2 : ln(1+x) = x - x²/2 + o(x²)

La seconde approche part d'abord de g(x) = 1/(x+1)
et en cherche le DL à l'ordre 2 en 0, on arrive à : 1/(1+x) = 1 - x + x² + o(x²)
Ensuite, ils intègrent et arrivent à : ln(1+x) = x - x²/2 + x³/3 + o(x³)

Je ne sais pas ce qu'on enseigne en France et je me garderai bien de prendre parti pour l'une ou l'autre approche.

Si l'un ou l'autre des intervenants sait ce qu'on est censé faire en France, il pourra te renseigner.

Je me suis contenté de donner mon opinion de non matheux (du moins dans l'enseignement) qui a constaté en de très multiples reprises que la notion de consensus des mathématiciens sur les diverses conventions était très très loin d'exister.

[Wil Fried]

@Black-Jack Merci pour votre avis

[Black-Jack]

@Wil-Fried a dit dans Calcul de développement limité :

(1/e)[(1+x)^((x+2)/2x)]

Rebonjour,

Pour la suite ...

$f(x)=\frac{1}{e}\ast (1+x{)}^{\frac{x+2}{2x}}$

$f^{\prime }(x)=(x+1{)}^{\frac{2-x}{2x}}\ast \frac{x(x+2)-2(x+1).ln(x+1)}{2e.x^2}$

$f^{\prime \prime }(x)=(x+1{)}^{\frac{2-3x}{2x}}.\frac{-(x^2+8x+4).x^2+4(x+1)\ast x^2.ln(x+1)+4(x+1{)}^2.l{n}^2(x+1)}{4e.x^4}$

J'ai fait calculer les limites par mon singe qui trouve :

$li{m}_{x\to 0}f(x)=1$

$li{m}_{x\to 0}{f}^{\prime }(x)=0$

$li{m}_{x\to 0}{f}^{\prime \prime }(x)=\frac{1}{6}$

Et donc : $\frac{1}{e}\ast (1+x{)}^{\frac{x+2}{2x}}=1+0+\frac{1}{6}\ast \frac{x^2}{2!}+o(x^3)$

$\frac{1}{e}\ast (1+x{)}^{\frac{x+2}{2x}}=1+\frac{x^2}{12}+o(x^3)$

Réponse différente de la tienne ... et aussi de celle que tu donnes dans le corrigé (erreur de signe)

J'ai donc recherché un site qui calcule en ligne les DL
https://www.codabrainy.com/taylor/

et voici ce qu'il donne :

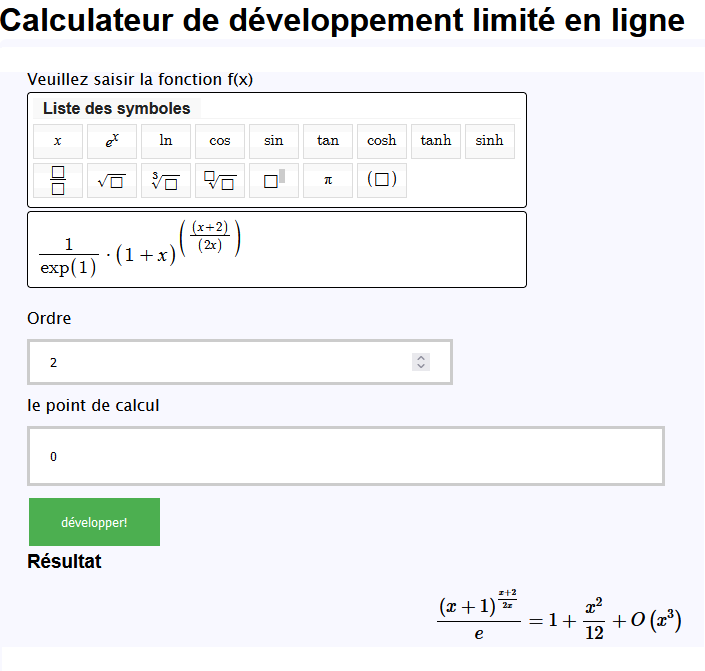
Conforme à ce que j'avais trouvé.

[mtschoon]

Bonjour,

Tout à fait d'accord avec la réponse de Black-Jack sur le DL de f(x) donné.
Il y a visiblement une erreur dans la correction ou lorsque @Wil-Fried a recopié la réponse trouvée dans la correction.

@Wil-Fried , je vais essayer de t'expliquer pourquoi ta réponse $1-\frac{x^2}{4}$, bien qu'il n'y ait pas d'erreur de calcul, ne représente pas un DL d'ordre 2. D'ailleurs, si on regarde l'énoncé (pas la correction, l'énoncé) on te demande le DL de f(x) d'ordre 1 au voisinage de $0$

Tu as d'abord trouvé , à la question 1, pour $ln(1+x)$
$ln(1+x)=x-\frac{1}{2}{x}^2+o(x^2)$ C'est OK.
Je suppose que tu as utilisé ensuite $x-\frac{1}{2}{x}^2$ pour faire les transformations relatives à $f(x)$ et tu as trouvé $1-\frac{x^2}{4}$ mais, avec cette expression, il n'y a pas de "reste", donc cette expression ne correspond pas à un DL.
Avec cette expression, tu aurais pu donner le DL à l'ordre 1 de $f(x)$ : $f(x)=1+o(x^2)$
(j'ai écrit $o(x^2)$ vu qu'il n'y a pas de terme de degré 1).

Avec ce DL , tu peux sans sans difficulté prouver la continuité de f en 0 et la dérivabilité de f en 0, et tu trouves $f^{\prime }0)=0$.

[mtschoon]

@Wil-Fried ,
A la correction, tu dis que "ils sont allés à l'ordre 3"
$ln(1+x)=x-\frac{x^2}{2}+\frac{x^3}{3}+o(x^3)$
Je pense (?) qu'ils ont fait les calculs avec $x-\frac{x^2}{2}+\frac{x^3}{3}$ pour transformer $f(x)$ , qu'ils ont tronqué le terme en $x^3$, et qu'ils ont pu (ou qu'ils auraient dû ) écrire :
$f(x)=1+\frac{x^2}{12}+o(x^3)$

Bien sûr, avec cette expression, on peut prouver que :

$\underset{x\to 0}{\lim }f(x)=1=f(1)$ donc $f$ continue en $0$

$\underset{x\to 0}{\lim }\frac{f(x)-f(0)}{x-0}=\underset{x\to 0}{\lim }\frac{f(x)-1}{x}=0$

donc f dérivable en $0$ et $f^{\prime }(0)=0$

[mtschoon]

@Wil-Fried ,
Si tu veux une illustration graphique de la continuité et de la dérivabilité de f en $0$, regarde :

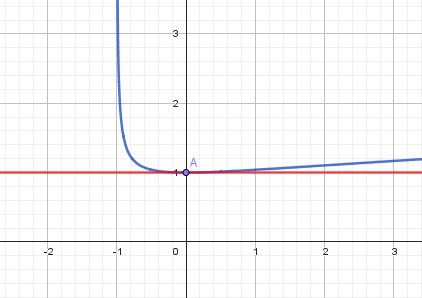
La droite en rouge d'équation $y=1$ et la tangente à la courbe en A point de coordonnées ($0,1)$

Si tu as besoin d'un cours sur les DL, tu peux regarder ici
https://homeomath2.imingo.net/devlim.htm
Bien sûr, on en trouve un peu partout sur le web, mais je trouve celui là simple et clair.

Bon travail !