Ensemble quotient nombre premier

Salut à vous. S’il vous plaît j’aimerais avoir de l’aide sur cet exercice.

Soit l’équation $x^{3}-x^{2}-2x=0$ .
a) Résoudre cette équation dans $Z / 6 Z$ et dans $R$ . Comparer.
b) Étant donné un nombre premier p, résoudre l’équation dans $Z / p Z$ .

J’ai pu répondre à la première question mais mon problème se situe au niveau de la question (b). Merci d’avance.

@Josias , bonjour,

Seulement quelques réflexions.

Tu ne dis pas la méthode que tu as utilisé pour la question 1)

Dans $R$ , tu as pu factoriser : $x(x−2)(x+1)=0\boxed{x(x-2)(x+1)=0}$
Comme $R$ est un corps, donc intégre, un produit de facteurs est nul ssi un des facteurs est nul

Par contre, $Z / 6 Z$ n'est pas intègre car $6$ n'est pas premier.
Tu as dû passer en revue les 6 cas $(x=0ˉ,x=1ˉ,x=2ˉ,x=3ˉ,x=4ˉ,x=5ˉ)(x=\bar{0}, x=\bar{1},x=\bar{2},x=\bar{3},x=\bar{4},x=\bar{5})$ et tiré la conclusion.

Lorsque $p$ est premier , $Z / p Z$ est un corps donc intègre , dans $Z / p Z$ , un produit de facteurs est nul ssi un des facteurs est nul.
Tu peux donc utiliser la factorisation proposée et répondre directement (facteurs nuls)

@mtschoon
Merci infiniment pour votre attention et je voudrais également vous présenter mes excuses. Concernant la première question, j’ai pu trouver des solutions pour l’équation dans $Z / 6 Z$ en faisant un tableau (Malheureusement je ne puis vous le montrer sur le forum).Les solutions sont :$ 0,2,5$ dans l’ensemble $Z / 6 Z$ .
Concernant la factorisation, je l’ai fait pour résoudre l’équation dans $R$ . Mais ce que je ne comprends toujours pas c’est au niveau de la question (2). Si toutefois j’ai bien répondu à la première question. Merci à vous.

@Josias , bonsoir,

Pour la 1), effectivement, ce serait mieux d'avoir donné ton tableau pour $Z / 6 Z$
$Z / 6 Z$ n'est pas intègre.

Pour le tableau, tu as pu faire une ligne pour $x$ (prenant les valeurs $0ˉ,1ˉ,...,5ˉ)\bar{0},\bar{1},...,\bar{5})$ , une pour $x^3$ , une pour $x^2$ , une pour $2 x$ puis une pour $x^2-x^2-2x$

Tu as pu aussi faire le tableau avec le produit, mais dans ce cas , vu que $Z / 6 Z$ n'est pas intègre. tu peux éventuellement trouver un produit nul alors que les 3 facteurs ne sont pas nuls ("diviseurs de zéro")

Vérifie ton tableau car je me demande si $3ˉ\bar{3}$ ne fait pas partie des solutions...

Pour la 2), tu utilises la factorisation faite car, vu que $p$ est premier, $Z / p Z$ est intègre, un produit de facteurs est nul si et seulement si un des facteurs est nul, donc pas besoin de faire un tableau.

L'équation équivaut à :

$x=0ˉx=\bar{0}$ ou $x−2ˉ=0x-\bar{2}=0$ ou $x+1ˉ=0ˉx+\bar {1}=\bar{0}$

Si tu as beaucoup de partience (il en faut !), tu peux consulter ici :
https://www.youtube.com/watch?v=-v3owWJMb-w

@Josias , pour la 1) , cas de $Z / 6 Z$ , je te joins un tableau fait avec le produit des 3 facteurs.

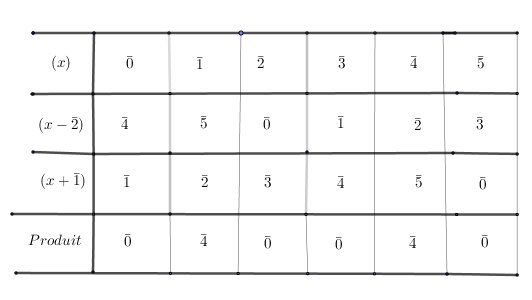
Vérifie.

@Josias ,

J'espère que tu as regardé tout ça de près et que pour la 2) tu as trouvé : $,p−1‾\bar{0}\ ,\bar{2}\ ,\overline{p-1}$

Bon travail.