Lois de composition interne

Salut, alors on a F={1, 2, 3, 4, 5}
et je dois ecrire la table d'une lois de composition interne et commutative sur F admettant 2 pour element neutre
ensuite 3 pour element neutre mais tels que 2 soit le symetique de 1

@Maxence
Car 2 est neutre, c'est à dire Ao2=2oA=2, donc la table doit avoir linge 2 et colonne 2 doivent être 2. Par conséquent 1o2=2o1=2 donc 1 et 2 sont automatiquement symétriques. Les autres lignes et colonnes sont libres mais il faut être AoB=BoA (commutatif), une dans des solutions est
o 1 2 3 4 5
1 1 2 3 4 5
2 2 2 2 2 2
3 3 2 1 2 3
4 4 2 2 3 4
5 5 2 3 4 5

Pour 3 est neutre, comme la même méthode dessus, la table doit avoir linge 3 et colonne 3 doivent être 3. Pour 1 et 2 sont symétriques, on doit mettre 1o2=2o1=3 . Les autres lignes et colonnes sont libres mais il faut être AoB=BoA, une dans des solutions est
o 1 2 3 4 5
1 1 3 3 4 5
2 3 2 3 2 2
3 3 3 3 3 3
4 4 2 3 3 4
5 5 2 3 4 5

Bonjour,

@ufeel , c'est gentil de vouloir aider , mais les tableaux que tu proposes sont faux, car tu as fait une confusion au sujet de l'élément neutre (une ligne et une colonne sont fausses dans chacun des 2 tableaux que tu donnes).

Rappel : soit $e$ l'élément neutre de la loi $o$
$x=x\boxed{\forall x \in F, x\ o\ e=e\ o\ x=x}$

Voir : https://lexique.netmath.ca/element-neutre/

@Maxence , piste pour le premier tableau

J'ai noté * la loi de composition interne

Par définition de l'élément neutre $2$ :
$∀x∈F\forall x\in F$ , x * 2 = 2 * x = x
Ainsi, tu remplis, comme fait sur le schéma que je te donne, la ligne $2$ et la colonne $2$

Tu remplis avec ce que tu souhaites (éléments de F , bien sûr) les $4$ cases vides en diagonale (trait rouge)

Tu remplis ensuite les 6 cases vides d'une des 2 parties triangulaires en mettant ce que tu souhaites (éléments de F , bien sûr)

Vu que la loi * doit être commutative, c'est à dire :
$∀a,b∈F\forall a, b \in F$ : a * b = b * a , tu replis la seconde partie triangulaire par symétrie par rapport à la diagonale (trait rouge)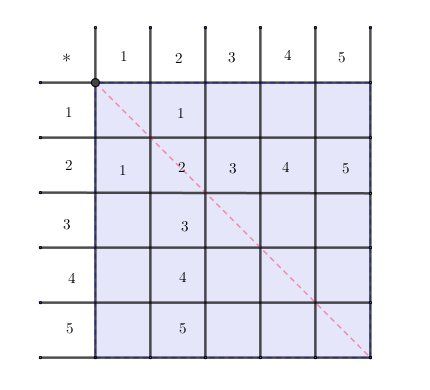

Reposte si ce n'est pas clair.

@Maxence , piste pour le second tableau

J'ai noté * la loi de composition interne

Par définition de l'élément neutre $3$ :
$∀x∈F\forall x \in F$ , x * 3 = 3 * x = x
Ainsi, tu remplis, comme fait sur le schéma que je te donne, la ligne $3$ et la colonne $3$

Par définition, $a^{'}$ symétrique de $a$ , l'élément neutre étant $3$ , veut dire que : a * a' = a' * a = 3

Ici , il faut : 2 * 1 =1 * 2 = 3
Tu remplis donc, comme fait sur le schéma que je te donne, la case $(1, 2)$ et la case $(2, 1)$ avec $3$

Ensuite, tu remplis les $14$ cases vides restantes avec ce que tu souhaites (éléments de F , bien sûr) , vu que la loi n'est pas commutative.

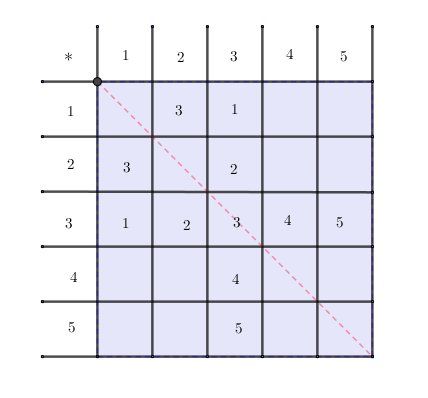
Reposte si ce n'est pas clair.

@mtschoon wow c'est intelligent, merci, j'y ai reflichis et jai trouver ce qu'il fallait faire par contre ta methode fais gagner beaucoup de temps

merci pour tes deux reponses mtschoon

De rien @Maxence , c'était avec plaisir !

C'est parfait si mes pistes t'ont étaient utiles.