Intégral double avec changement de variable
-
Walid LELLOUCHI dernière édition par Walid LELLOUCHI
bonsoir a vous ,voici cette intégrale qui est particulièrement simple mais je me demandez pourquoi en ne peut pas choisir ces intervalle pour r et thêta comme montré dans la pièce joint c'est la 6eme
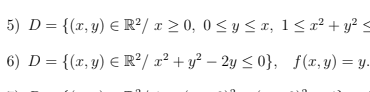
-
mtschoon dernière édition par mtschoon

Bonjour,
@Walid-LELLOUCHI a supprimé sa question après avoir eu une réponse ! ! !
Elle a été ré-activée par @Casebas.Pour que les consultants puissent comprendre de quoi il s'agit dans la cas où @Walid-LELLOUCHI recommencerait à la supprimer (!) , je résume "approximativement" cette question :
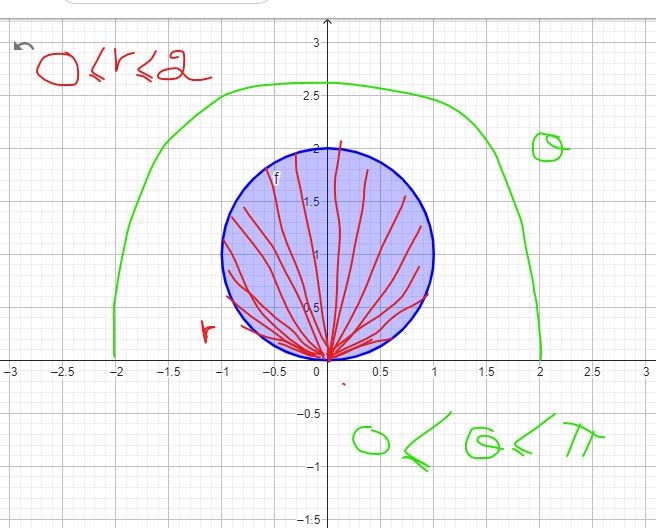
Savoir pourquoi il n'est pas possible de faire le changement de variables (rrr, θ\thetaθ ) pour calculer l'intégrale double suivante , avec le schéma joint :
DDD= { (x,y)∈R2/x2+y2−2y≤0(x,y)\in R^2/x^2+y^2-2y\le 0(x,y)∈R2/x2+y2−2y≤0 } ,f(x,y)=y, f(x,y)=y,f(x,y)=y
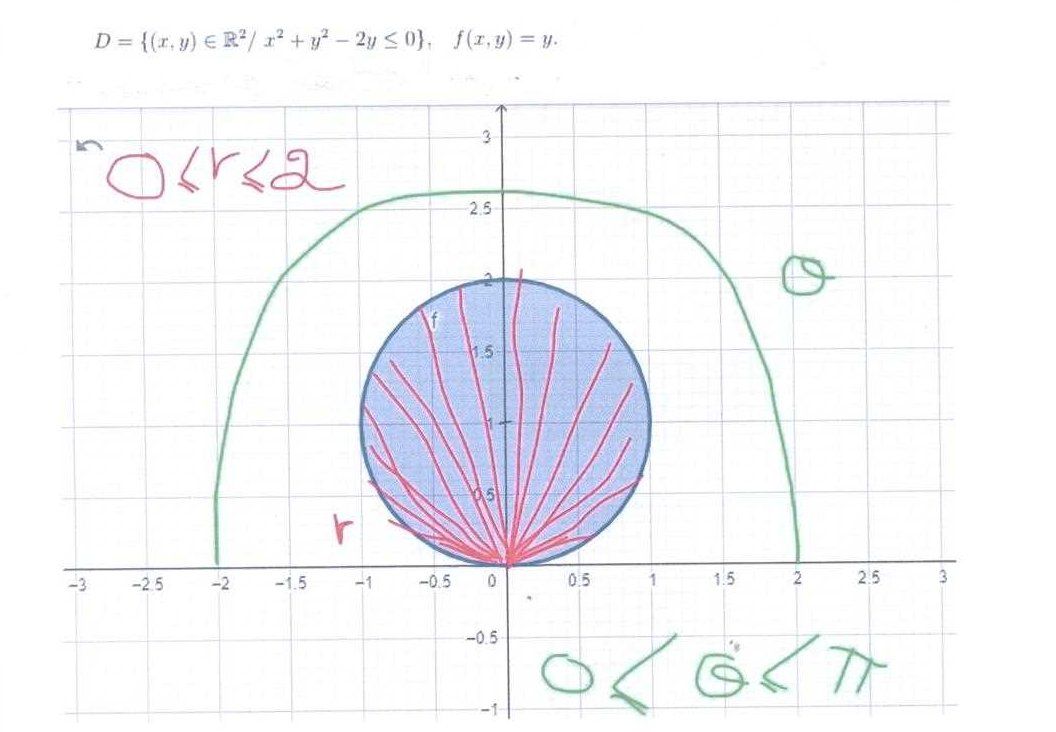
Réponse donnée à cette question, à @Walid-LELLOUCHI :
Si tu parles d'un domaine défini par des variables indépendantes θ\thetaθ et rrr avec :
0≤θ≤π0\le \theta\le \pi0≤θ≤π et 0≤r≤20\le r\le 20≤r≤2, il s'agit du demi-disque en bleu que je te joins.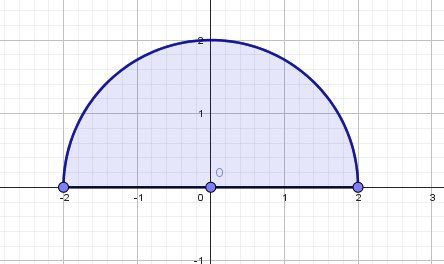
Si c'était cela ton but pour le calcul , ce n'est effectivement pas possible , carce domaine ne correspond pas au domaine de la question que tu indiques (où θ\thetaθ et rrr ne peuvent pas être indépendantes).Remarque :
@Walid-LELLOUCHI s'est trompé de rubrique car les intégrales doubles ne sont pas au programme (français) de Terminale. Elles se traitent en Supérieur.
-
mtschoon dernière édition par

Bonsoir,
Merci à la modération d'avoir déplacer ce topic.
-
mtschoon dernière édition par mtschoon

Bonjour,
Merci à @Casebas d'avoir re-activé l'énoncé (effacé par Walid LELLOUCHI , après avoir eu une réponse).