Matrices carrées d'ordres 3.

Bonjour j'espère que vous vous portiez bien.
J'ai un exercice dont je bloque dessus ,j'aimerais avoir besoin de votre aide.
Exercice :
( 0 0 0 )
Soit Aα= (-2 1 -1 )
(2 0 α )
une matrice carrée , avec α ∈ℝ.

Calculer (Aα)³ - 3(Aα)² + 2Aα en fonction de α.
Trouver α pour que (Aα)³ - 3(Aα)² +2Aα soit égale à la matrice carrée nulle d'ordre 3.
Soit n un entier naturel non nul.
a) Calculer les racines réelles de X³ - 3X² + 2X
b ) Calculer le reste de la division euclidienne de Xⁿ⁻¹ par X³ -3X² + 2X en fonction de n.
c ) En supposant que A₂ est une matrice de X³ -3X² + 2X, calculer (A₂)ⁿ.
Je vous remercie pour vos réponses d'aide .

@medou-coulibaly , bonjour,

Je te donne des indications globales, pour t'aider à travailler ton exercice, mais c'est à toi de le faire.

1 ) Tu as déjà fait ce genre de calculs dans l'exercice que tu as posté dernièrement.
Tu calcules $(Aα)2(A_\alpha)^2$ , puis $(Aα)3(A_\alpha)^3$ puis l'expression proposée.
Sauf erreur, tu dois trouver :
$α3−3α2+2α)\begin{pmatrix} 0\ \ \ \ \ 0\ \ \ \ \ 0\cr 4-2\alpha\ \ \ \ \ 0\ \ \ \ 2\alpha-\alpha^2 \cr 2\alpha^2-6\alpha+4\ \ \ \ 0\ \ \ \ \alpha^3-3\alpha^2+2\alpha\end{pmatrix}$

2 ) Avec l'expression du 1), tu dois trouver $α=2\alpha=2$

3 )a) $X^3-3X^2+2X=X(X^2-3X+2)$

$X^3-3X^2+2X=0$ <=> $X = 0, X = 1, X = 2$

3 )b) Ton énoncé parle de $X^{n-1}$
Cela me surprend car dans la question suivante, il s'agit de $A_2)^n$
Je te donne des pistes pour calculer le reste de la division euclidienne de $X^n$ par $X^3 -3X^2 + 2X$
$X^n=Q(X)(X^3-3X^2+2X)+R(X)$
Nécessairement, $degreˊ(R(X))<degreˊ(X3−3X2+2X)degré(R(X))\lt degré(X^3-3X^2+2X)$
Donc : $R(X)=aX^2+bX+c$
$Xn=(X3−3X2+2X)Q(X)+aX2+bX+c\boxed{X^n=(X^3-3X^2+2X)Q(X)+aX^2+bX+c}$
Il faut trouver $a, b, c$

Idée : Donner à $X$ les valeurs $0, 1, 2$ qui annulent $X^3-3X^2+2X$

Ainsi, avec la formule encadrée :
pour $X = 0$ on obtient $0 = c$
pour $X = 1$ on obtient $1 = a + b + c$
pour $X = 2$ on obtient $2^n=4a+2b+c$

Après résolution sauf erreur , on trouve :
$c=0, b=2-2^{n-1},a=2^{n-1}-1$

Ainsi : $R(X)=(2n−1−1)X2+(2−2n−1)X\boxed{R(X)=(2^{n-1}-1)X^2+(2-2^{n-1})X}$

Remarque : si c'est vraiment $X^{n-1}$ qui est demandé, tu peux le faire, et ensuite , tu multiplieras par $X$ pour obtenir $X^n$ nécessaire à la dernière question.

La question 3 )c), qui est le but de l'exercice, se traite en remplaçant $X$ par $A_2$

Bon travail.

@mtschoon Bonjour madame j'ai compris je vais travailler dessus

Bon travail @medou-coulibaly .
Reposte si besoin.

@mtschoon Bonjour madame, j'espère que vous allez bien !
Madame jusque-là j'ai du mal à démarrer

@mtschoon je rencontre des toujours des difficultés même après vos pistes données.

@medou-coulibaly ,bonjour,

Merci de préciser ce qui te bloque.

@mtschoon je bloque sur le calcule de (Aα)² et (Aα)³, puis de l'expression proposée.
Quand je calcule je tombe pas sur le même résultat que le vôtre

@medou-coulibaly ,

Si besoin, je t'indique les valeurs, en principe exactes, de $(Aα)2(A_\alpha)^2$ et $(Aα)3(A_\alpha)^3$

Je t'avais indiqué un lien où tu peux vérifier les calculs en ligne:
https://www.dcode.fr/simplification-mathematique

Je te joins les réponses.
Il faut bien sûr que tu remplaces $a$ par $α\alpha$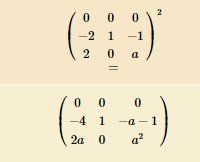

matrice au carré.jpg

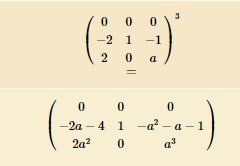
matrice au cube.jpg

Bons calculs.

@mtschoon maintenant la deuxième question comment vous avez fait pour trouver α=2

@medou-coulibaly ,

Pour la 2)
La matrice 3x3 nulle est composée de 9 zéros.
Tu dois donc résoudre le système :

${4−2α=02α−α2=02α2−6α+4=0α3−6α2+2α=0\begin{cases}4-2\alpha=0\cr 2\alpha-\alpha^2=0\cr 2\alpha^2-6\alpha+4=0\cr\alpha^3-6\alpha^2+2\alpha=0\end{cases}$

La première équation $4−2α=04-2\alpha=0$ te donne $α=2\alpha=2$

Ensuite, tu vérifies que cette valeur $2$ convient aux trois autres équations

@mtschoon merci Madame, maintenant la 3 b ) j'ai du mal à comprendre votre explication

@medou-coulibaly ,

Pour la 3) b) , il faudrait que tu commences à assimiles ton cours sur sa division euclidienne des polynômes.
Si besoin, regarde ici
https://fr.wikipedia.org/wiki/Division_d'un_polynôme

Dans ton exercice , j'ai utiliser $X^n$ ce qui est commode pour la dernière question, mais lorsque tu auras compris, tu pourras utiliser $X^{n-1}$ si c'est cela qui est écrit dans ton énoncé, bien que cela paraisse un peu bizarre...)

Je t'explique donc avec $X^n$

Je te mets la disposition pratique (comme la division des nombres réels) de $X^n$ par le polynôme $X^3-3X^2+2X$ : le quotient est le polynôme $Q (X)$ et le reste est le polynôme $R (X)$

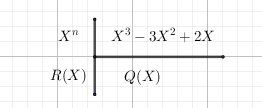
Cela se traduit par :
$Xn=[(X3−3X2+2X)×Q(X)]+R(X)X^n=\biggr[(X^3-3X^2+2X)\times Q(X)\biggr]+R(X)$

avec $(X3−3X2+2X)degré\ de \ R(X) \lt degré \ de\ (X^3-3X^2+2X)$

$R (x)$ est donc un polynôme de degré au plus égal à $2$ , c'est à dire $R(X)=aX2+bX+c\boxed{R(X)=aX^2+bX+c}$

Essaie de comprendre seul la fin de l'explication que je t'ai donnée pour trouver les valeurs de $a, b, c$

Si tu comprends pas, je t'expliciterai davantage mais ce serait mieux que tu arrives à le comprendre seuL

@mtschoon ok madame au fur et à mesure je suis là travaillé dessus en même temps.
La 3 c ) j'ai du mal à remplacer X par A₂

@medou-coulibaly ,

Piste pour la 3)c)

Tu remplaces $X$ par $A_2$ dans la réponse de la 3)b)

$(A2)n=[(A2)3−3(A2)2+2A2]Q(A2)+R(A2)(A_2)^n=\biggr[(A_2)^3-3(A_2)^2+2A_2\biggr]Q(A_2)+R(A_2)$

Or, tu sais [voir Question 2] que $A_2)^3-3(A_2)^2+2A_2=$ "0" (en appelant "0" la matrice nulle )

Il reste donc : $A_2)^n=R(A_2)$

En remplaçant $R_2$ par son expression [voir question 3)b) ]

$(A2)n=(2n−1−1)(A2)2+(2−2n−1)A2\boxed{(A_2)^n=(2^{n-1}-1)(A_2)^2+(2-2^{n-1})A_2}$

Si tu veux l'expression matricielle de $A_2)^n$ , tu remplaces $A_2)^2$ et $A_2$ par leurs expressions matricielles et tu termines le calcul.

@mtschoon ok merci beaucoup madame j'ai compris

De rien @medou-coulibaly .

C'est très bien si tu es arrivé à terminer ton exercice.

@mtschoon
Merci à vous madame

De rien et bon travail @medou-coulibaly