DM.Développement limité et calcule de limites

Bonjour comment vous allez ? J'ai un exercice dont je bloque sur la résolution, j'aimerais besoin d'aide de votre part.

a) Donner le développement limité de ln(cosx) à l'ordre 2.
b) Calculer lim( x-->0) [( 1+x)/ cosx ]^a/x
Calculer lim( x ---> ∞) [ 1-2/x] ^ ax

Bonjour,

a)

f(x) = ln(cos(x))
f'(x) = -sin(x)/cos(x) = -1/tan(x)
f''(x) = -1/cos²(x)

f(0) = 0
f'(0) = 0
f''(0) = -1

DL : -x²/2 + o(x³)
'''''''''
b)
g(x) = [(1+x)/cos(x)]^(a/x)

ln(g(x)) = (a/x).(ln(1+x) - ln(cos(x))

Et, près de 0 avec la partie 1a :

$\simeq a.\frac{ln(1+x)}{x} - \frac{a}{x}.\frac{-x^2}{2}$

$\simeq a.\frac{ln(1+x)}{x} + \frac{a.x}{2}$

$limx→0ln[(1+xcos(x))ax]≃limx→0a.ln(1+x)x+limx→0a.x2lim_{x\to 0} ln[(\frac{1+x}{cos(x)})^{\frac{a}{x}}] \simeq lim_{x\to 0} a.\frac{ln(1+x)}{x} + lim_{x\to 0} \frac{a.x}{2}$

$limx→0ln[(1+xcos(x))ax]≃a∗1+0lim_{x\to 0} ln[(\frac{1+x}{cos(x)})^{\frac{a}{x}}] \simeq a*1 + 0$

$limx→0ln[(1+xcos(x))ax]≃alim_{x\to 0} ln[(\frac{1+x}{cos(x)})^{\frac{a}{x}}] \simeq a$

Et donc $limx→0[(1+xcos(x))ax]=ealim_{x\to 0} [(\frac{1+x}{cos(x)})^{\frac{a}{x}}] = e^a$

A vérifier et à toi pour le 2ème.

@Black-Jack Bonjour monsieur, merci beaucoup je fais mais je n'arrive pas à avoir une issue

@medou-coulibaly a dit dans DM.Développement limité et calcule de limites :

@Black-Jack Bonjour monsieur, merci beaucoup je fais mais je n'arrive pas à avoir une issue

Il faut essayer ... par exemple :

Poser x = 1/t (et donc x--> +oo correspond à t --> 0)

lim(x--> +oo) [ 1-2/x]^(a.x) = lim(t--> 0) [1-2t]^(a/t)

f(t) = [1-2t]^(a/t)
ln(f(t)) = a/t * ln(1-2t)

DL en 0 de ln(1-2t) ... à faire.
On trouve : ln(1-2t) = -2t + O(t²)

Et donc
$[at∗ln(1−2t)]=limt→0[at∗(−2t)]=−2alim_{t\to 0 }\ [\frac{a}{t} * ln(1-2t)] = lim_{t\to 0} [\frac{a}{t} * (-2t)] = -2a$

Et donc $limt→0[1−2t]a/t=e−2alim_{t\to 0 } [1-2t]^{a/t} = e^{-2a}$

$limx→+∞[1−2x]a.x=e−2alim_{x\to +\infty } [1-\frac{2}{x}]^{a.x} = e^{-2a}$

@Black-Jack ok d'accord c'est compris monsieur

@medou-coulibaly merci beaucoup pour votre aide

@Black-Jack je n'arrive pas à avoir le DL en 0 de ln(1-2t) ...

f(t) = ln(1-2t)
f'(t) = -2/(1-2t)
f''(t) = -4/(1-2t)²

f(0) = 0
f'(0) = -2
f''(0) = -4

DL d'ordre 1 en 0 de ln(1+t) : 0 - 2t + o(t²) = -2t + O(t²)

@Black-Jack ok merci beaucoup monsieur

@Black-Jack Bonjour monsieur je pense qu'il n'y eu une petite erreur sur la 1-a )
DL : -x²/2 + o(x³)
Je pense que ça fait DL : -x²/2 + o(x²) car on dit le DL à l'ordre 2

@medou-coulibaly a dit dans DM.Développement limité et calcule de limites :

@Black-Jack Bonjour monsieur je pense qu'il n'y eu une petite erreur sur la 1-a )
DL : -x²/2 + o(x³)
Je pense que ça fait DL : -x²/2 + o(x²) car on dit le DL à l'ordre 2

Bonjour,

Voila ce que donnent deux logiciels en ligne de calcul de DL (qui trouvent le même résultat que celui que j'avais donné) :

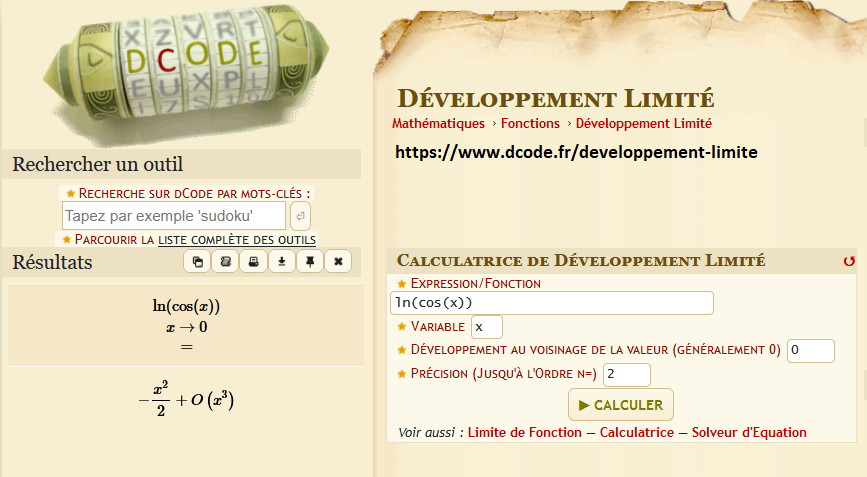
Sans titre1.png

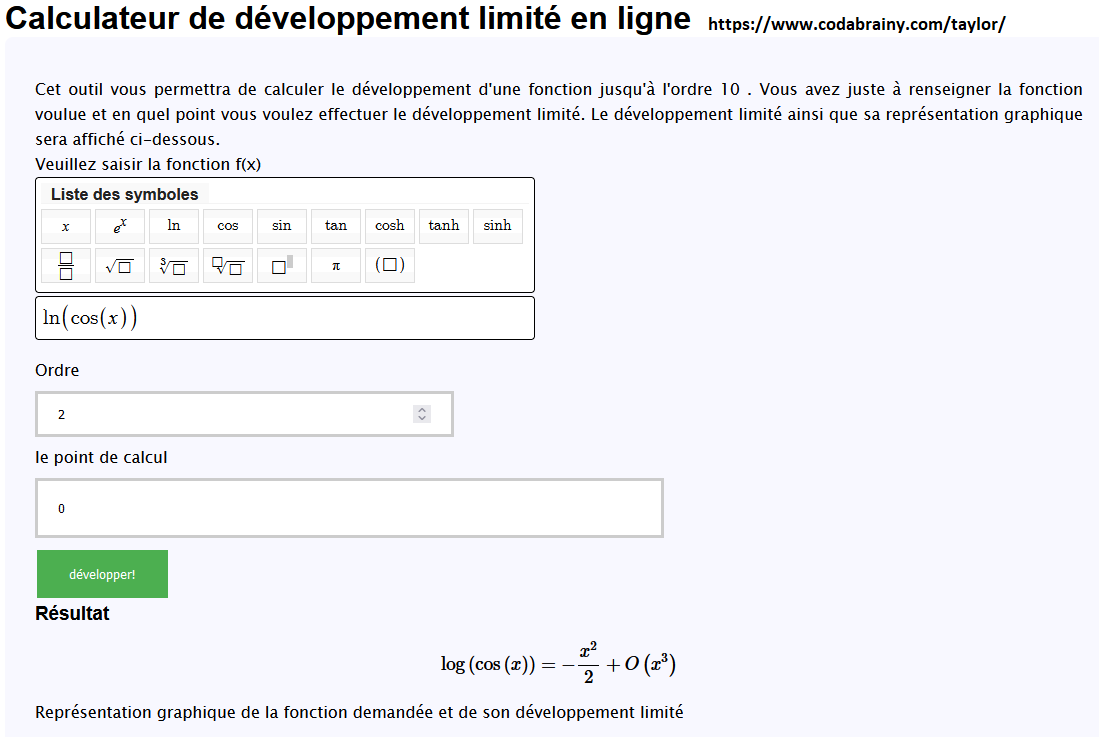
Sans titre.png

@Black-Jack ok merci beaucoup

Bonsoir,

Je viens de regarder la fin de ce topic .

A propos du "petit o" et "grand O", il y a une nuance.

Dans le calculateur DCODE, il ne s'agit pas visiblement du "petit o"...

De façon usuelle , en maths, on utilise le "petit o"

(Le "grand O" est plutôt utilisé en informatique et n'a pas tout à fait la même signification mathématique)

Pour l'usage du "petit o", je mets un lien à consulter, qui en donne toute l'explication et qui doit correspondre au cours de medou-coulibaly :

https://www.methodemaths.fr/developpements_limites/#petito

Formule de Taylor-Young : développement limité de f à l’ordre n au voisinage de a :

$f(x)=f(a)+f′(a)(x−a)+f′′(a)2!(x−a)2+...+f(n)(a)n!(x−a)n+o(x−a)nf(x)=f(a)+f'(a)(x-a)+\dfrac{f''(a)}{2!} (x-a)^2+...+\dfrac{f^{(n)}(a)}{n!} (x-a)^n+o(x-a)^n$

En particulier au voisinage de 0 :
$f(x)=f(0)+f′(0)x+f′′(0)2!x2+...+f(n)(0)n!xn+o(xn)\boxed{f(x)=f(0)+f'(0)x+\dfrac{f''(0)}{2!} x^2+...+\dfrac{f^{(n)}(0)}{n!} x^n+o(x^n)}$

La remarque de @medou-coulibaly est bien exacte , avec le "petit o", bien sûr.

Bonne nuit, vu l'heure tardive.

@mtschoon

Bonjour,

J'ai malencontreusement tapé "o" à la place de "O" dans mon premier message.

J'ai été moins distrait dans les autres, où j'ai bien indiqué "O".

Par exemple :
DL en 0 de ln(1-2t) ... à faire.
On trouve : ln(1-2t) = -2t + O(t²)

@Black-Jack oui je trouve ça je pense bien

@mtschoon Bonjour/Bonsoir madame

@medou-coulibaly , bonjour,

J'espère que tu n'es par géné les "petits o" et les "grands O"

Je te rappelle quelques définitions, si besoin (pour savoir exactement de quoi on parle lorsqu'on les utilise)

Au voisinage d'un point,
$f (x) = o (g (x))$ veut dire que $f(x)g(x)\dfrac{f(x)}{g(x)}$ tend vers $0$
$f (x) = O (g (x))$ veut dire que $∣f(x)g(x)∣|\dfrac{f(x)}{g(x)}|$ est borné
$\sim g(x)$ veut dire que $f(x)g(x)\dfrac{f(x)}{g(x)}$ tend vers $1$

Bon travail !

@mtschoon Bonjour madame merci beaucoup je comprends bien