Bonjour, Je cherche la solution de cette équation différentielle: x.Y"+Y'-Y=0 Merci infiniment pour vos réponses.

Bonjour,

Il n'y a pas de solutions utilisant des fonctions élémentaires.
Cela nécessite des fonctions spéciales (fonctions de Bessel modifiées, dont on parle sur ce lien : https://fr.wikipedia.org/wiki/Fonction_de_Bessel_modifiée )

Ce n'est absolument du niveau Terminale S.

D'où vient cette équation ? Elle ne peut pas émaner d'un prof du Secondaire.

Si c'est toi qui l'a trouvée en essayant de résoudre un problème donné à ton niveau ... alors il est probable que tu t'es trompé en établissant cette équation.

@Black-Jack je vous remercie infiniment monsieur pour votre réponse, mais ce n'est pas niveau terminale, je suis une prof et j'ai besoin de cette solution dans mes recherches. je vais m'informer sur cette méthode. Merci encore une fois.

Rebonjour,

Cela dépend de ce dont tu as besoin.

Si on connait la plage des x que l'on veut parcourir et les conditions initiales sur y et y', on peut aussi faire une résolution numérique (par petits incréments de x) avec un tableur.

En exemple, j'ai choisi, x variant dans [1 ; 5] et pris comme conditions initiales :
y(1) = 2 et y'(1) = -3

On a alors facilement ceci :

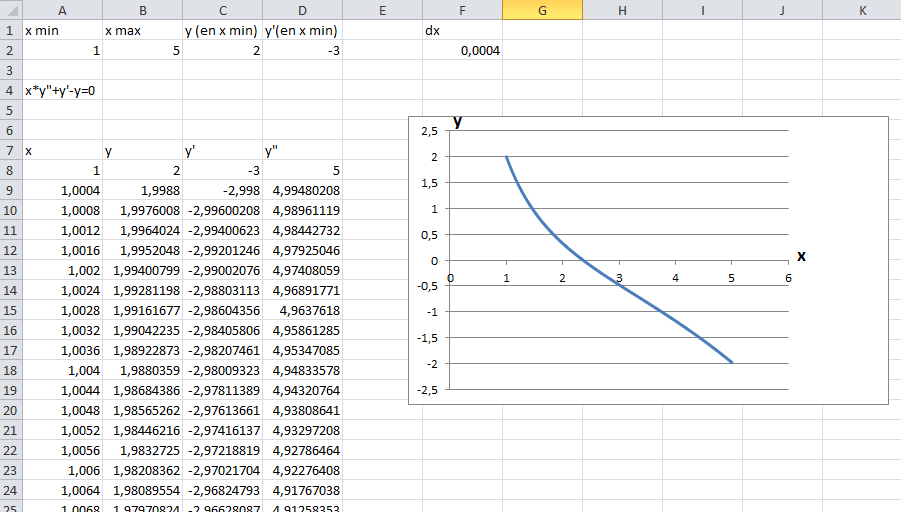
Sans titre.png

On peut évidemment modifier facilement la plage des x parcourues et les valeurs de y et y' pour x = x minimum