Fonction polynomiale et racine carré

Bonjour à tous,

Je travail depuis quelques temps à la résolution de cette équation :
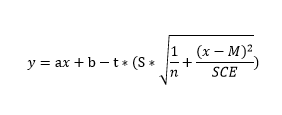
l'équation.png

Je cherche à remanier l'équation de la manière suivante Ax² + Bx + C avec :
A= l'ensemble des termes factorisant x²
B = l'ensemble des termes factorisant x
C = l'ensemble des autres termes

Afin d'avoir les solutions possibles de la fonction à l'aide des outils de résolution de fonction polynomiale de degré 2.
(B² - 4AC).

Le développement de cette équation est long et je bloque souvent sur la racine.
Je me demande également si il n'y aurais pas des identités remarquable que je n'aurais pas vu lorsque je développe.

Pourriez-vous m'aiguiller s'il vous plait ?

Merci beaucoup

@Pierre-Lancry

$t.S1n+(x−M)2SCE=ax+b−yt.S\sqrt{\frac{1}{n} + \frac{(x-M)^2}{SCE}} = ax + b - y$

Si ax + b - y est du signe contraire à t*S, il n'y a pas solution réelle.

Si ax + b - y est du signe de t*S, alors, on élève les 2 membre au carré.

$t2.S2∗(1n+(x−M)2SCE)=(ax+b−y)2t^2.S^2 * (\frac{1}{n} + \frac{(x-M)^2}{SCE}) = (ax + b - y)^2$

$t2.S2∗(1n+(x2+M2−2Mx)SCE)=a2x2+b2+y2+2abx−2axy−2byt^2.S^2 * (\frac{1}{n} + \frac{(x^2+M^2-2Mx)}{SCE}) = a^2x ^2+ b^2 + y^2 + 2abx - 2axy - 2by$

$x2∗(a2−t2S2SCE)+2x∗(ab−ay+Mt2S2SCE)+(b2+y2−t2.S2n−t2S2M2SCE)=0x^2 * (a^2 - \frac{t^2S^2}{SCE}) + 2x * (ab-ay + \frac{Mt^2S^2}{SCE}) + (b^2+y^2 - \frac{t^2.S^2}{n} - \frac{t^2S^2M^2}{SCE})= 0$

A vérifier, rien relu.