DM: Sous groupe distingué
-
DDonassi soungari Soro dernière édition par Donassi soungari Soro
Bonjour j'espère que vous allez bien. J'ai un exercice dont je bloque, j'ai besoin de votre aide Svp.
Soit G={ 1, -1, i , -i } le groupe de quatre nombres complexes en multiplication.
a) Est ce que { 1, -1 } est un sous groupe de G ? Si oui est-il distingués dans G , Pourquoi ?
b) Est ce que { 1 ,- i } est un sous de G? Pourquoi ? Quel est le Sous-groupe engendré par { -i } ?
J'ai besoin de votre aide svp.
-
mtschoon dernière édition par mtschoon

@Donassi-soungari-Soro , bonjour,
Quelques indications, mais je te laisse faire les calculs.
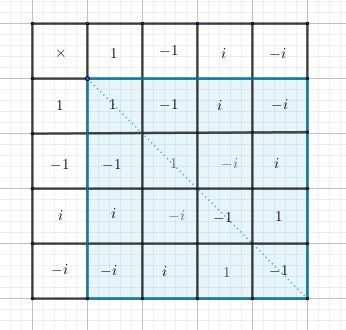
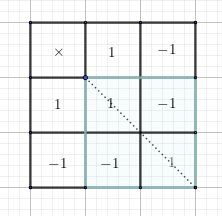
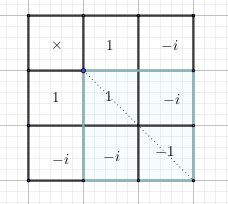
Pour les éclairer, je te suggère de faire les tables (multiplication) de G={1,-1,i,-i} ,H ={1,-1}et K={1,-i}
-
mtschoon dernière édition par mtschoon

a) Pour prouver que H={1,-1} est un sous groupe de G, le plus simple est d'utiliser une propriété caractéristique :
élément neutre 1∈H1 \in H1∈H (oui)
∀x,y∈H,xy−1∈H\forall x,y\in H, xy^{-1}\in H∀x,y∈H,xy−1∈H
tu as 4 calculs à faire :
1×(1)−1=1×1=11\times (1)^{-1}=1\times 1=11×(1)−1=1×1=1 etcHHH est distingué si et seulement si :
∀g∈G\forall g\in G∀g∈G et ∀h∈H\forall h\in H∀h∈H, ghg−1∈Hghg^{-1}\in Hghg−1∈H
hhh peut prendre 2 valeurs 1 et -1, et dans chacun de ces cas, tu calcules les valeurs de ghg−1∈Hghg^{-1}\in Hghg−1∈H et tu tires la conclusion.b) Pour prouver que K={1,-i} est un sous groupe de G , tu peux utiliser le même principe que pour HHH
Le sous groupe engendré par −i-i−i est l'intersection de tous les sous-groupes contenant −i-i−i.
Ces sous-groupes contiennent forcément l'élément neutre 111, donc ils contiennent forcément 111 et −i-i−iBons calculs
-
DDonassi soungari Soro dernière édition par
@mtschoon merci madame je vais vous faire part de mon calcul
-
DDonassi soungari Soro dernière édition par
@mtschoon après avoir calculer madame je trouve que { 1 , -1 } est un sous groupe et aussi distingué. Mais le deuxième n'est pas un SOS groupe
-
mtschoon dernière édition par

@Donassi-soungari-Soro , bonjour,
Je regarde les calculs.
Tes résultats me semblent bons.
Oui {1,-1} est un sous-groupe distingué.
Effectivement {1,-i} n'est pas un sous groupe.Le sous-groupe engendré par -i doit contenir 1 et -i.
Tu as donc 3 cas à étudier :
{1,-i,-1}
{1,-i , i}
{1,-i , i , -1}je pense que seul G={1,-i , i , -1} convient mais vérifie car j'ai fait vite.
-
DDonassi soungari Soro dernière édition par
@mtschoon merci beaucoup madame