inégalité de jensen, démo
-
-lala-o dernière édition par

Bonjour, afin de démontrer l'inégalité de Jensen, on nous a demandé de d'abord démontrer que
III={x=α1x1+α2x2\alpha_1 x_1 + \alpha_2 x_2α1x1+α2x2 / α1+α2\alpha_1 + \alpha_2α1+α2 = 1 , (αi\alpha_iαi) ∈\in∈ R0+R_0^+R0+ } = [x1;x2x_1 ; x_2x1;x2]
en utilisant les vecteurs ox1ox_1ox1 , ox2ox_2ox2 et x1x2x_1x_2x1x2. J'ai tenté de les représenter dans un graphe, mais je n'arrive pas à aller + loin.
-
BBlack-Jack dernière édition par Black-Jack
Bonjour,
Si j'interprète bien ce qui est demandé (ce qui n'est pas sûr) :
α1Ox1→+α2Ox2→\alpha_1 \overrightarrow{Ox_1} + \alpha_2 \overrightarrow{Ox_2}α1Ox1+α2Ox2
=α1Ox1→+(1−α1)Ox2→= \alpha_1 \overrightarrow{Ox_1} + (1-\alpha_1) \overrightarrow{Ox_2}=α1Ox1+(1−α1)Ox2
=α1(Ox1→−Ox2→)+Ox2→= \alpha_1 (\overrightarrow{Ox_1} - \overrightarrow{Ox_2}) + \overrightarrow{Ox_2}=α1(Ox1−Ox2)+Ox2
=α1x2x1→+Ox2→= \alpha_1 \overrightarrow{x_2x_1} + \overrightarrow{Ox_2}=α1x2x1+Ox2
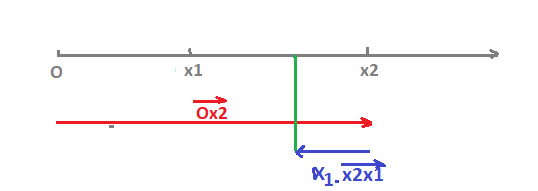
=Ox2→+α1.x2x1→= \overrightarrow{Ox_2} + \alpha_1 . \overrightarrow{x_2x_1}=Ox2+α1.x2x1 et comme 0 < alpha1 < 1 ... le point trouvé est dans [x1 ; x2]
-
-lala-o dernière édition par

@Black-Jack oui, c'est bien ça ! Merci beaucoup pour votre aide !