Calcul du volume du domaine de ℝ³

[medou coulibaly]

Bonjour comment vous allez, j'espère que vous allez bien.
Je bloque sur cet exercice dont j'ai besoin d'aide de votre part
Calcul le volume du domaine de ℝ³ : Δ = { ( x,y,z ) ∈ ℝ³ / √x + √y + √z ≤ 1

[Black-Jack]

Bonjour,

Intégrale triple ...

[medou coulibaly]

@Black-Jack Bonjour mais le signe ≤ 1 me cause soucis je ne sais pas ce que cela signifie

[Black-Jack]

@medou-coulibaly a dit dans Calcul du volume du domaine de ℝ³ :

@Black-Jack Bonjour mais le signe ≤ 1 me cause soucis je ne sais pas ce que cela signifie

Bonjour,
J'explique par un autre exemple :

Si au lieu de √x + √y + √z ≤ 1

on avait écrit : x² + y² + z² <= 1
La surface d'équation : x² + y² + z² = 1 est une sphère centrée sur l'origine du repère et de rayon 1

Le volume a chercher serait alors celui de la boule qui est "à l'intérieur" de cette sphère, surface extérieure de la sphère comprise ... donc le volume d'une boule de rayon 1.
Qu'on pourrait calculer par $2{\int }_0^{1}dx{\int }_{-\sqrt{1-x^2}}^{\sqrt{1-x^2}}dy{\int }_{-\sqrt{1-x^2-y^2}}^{\sqrt{1-x^2-y^2}}dz=...$
Pour une boule, on peut évidemment utiliser des méthodes autres que l'intégrale triple (puisque c'est un volume de révolution) ...

Mais dans le cas de l'exercice, une des rares méthodes est, je pense, l'homologue de celle faite ci-dessus ... en partant évidemment de √x + √y + √z ≤ 1 et pas de x²+y²+z² <= 1

[medou coulibaly]

@Black-Jack ok je vais calculer 2∫₀¹ dx
2∫₀¹ dx = 1/6

[medou coulibaly]

@Black-Jack ∫( -√(1- x^2) à √(1- x^2) ) dy
∫( -√(1- x^2) à √(1- x^2) ) dy = 0

[Black-Jack]

Bonjour,

J'ai donné un exemple avec une boule ...

Ce n'est pas ce que tu dois calculer ici.

Il faut appliquer une méthode semblable mais à partir des données de l'énoncé.

[medou coulibaly]

@Black-Jack mais je ne me retrouve pas hein

[Black-Jack]

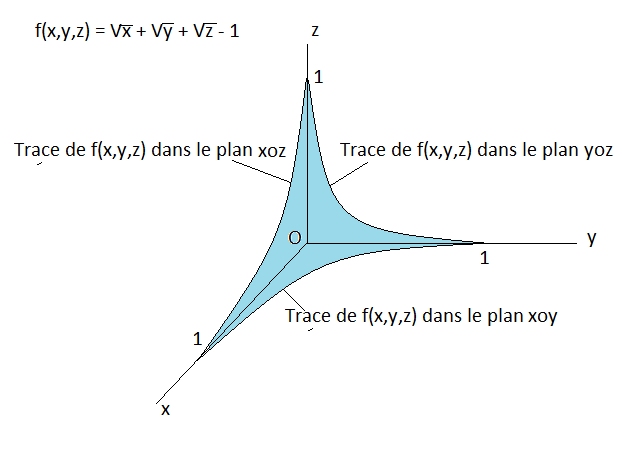
On te demande de calculer le volume "coincé" entre les plans oxy, oyz , oxz et la surface d'équation $f(x,y,z)=\sqrt{x}+\sqrt{y}+\sqrt{z}-1$

Volume en bleu sur le dessin.

[medou coulibaly]

@Black-Jack ok mais pouvez me guider comment ce calcul se fait ?

[Black-Jack]

$\sqrt{x}+\sqrt{y}+\sqrt{z}\le 1$ inplique que x, y et z sont dans [0 ; 1], en effet ils ne peuvent pas être négatifs sinon les racine carrée n'existeraient pas et si une (ou plusieurs) des variables étaient > 1, l'inégalité ne serait pas respectée.

Pour moi, on peut calculer le volume ainsi :

$V={\int }_0^{1}dx{\int }_0^{(1-\sqrt{x}{)}^2}dy{\int }_0^{(1-\sqrt{x}-\sqrt{y}{)}^2}dz$

Sauf distraction ou erreur.

[medou coulibaly]

@Black-Jack Bonsoir je trouve ceci
1/2× 1/2( √x-1)^4 × 1/2( √x+√y-1)^4
1/2 [ 1 × (√x-1)^4×(√x+√y-1)^4 ]

[Black-Jack]

Bonjour,

Je n'ai pas fait les calculs ...
Mais ta réponse n'est pas correcte, tu dois trouver une valeur numérique.

Cela doit ressembler à ce qui suit :

$V={\int }_0^{1}dx{\int }_0^{(1-\sqrt{x}{)}^2}(1-\sqrt{x}-\sqrt{y}{)}^{2}dy$

$V={\int }_0^{1}dx{\int }_0^{(1-\sqrt{x}{)}^2}(1+x+y-2\sqrt{x}-2\sqrt{y}+2\sqrt{xy.})dy$

$V={\int }_0^{1}dx{\int }_0^{(1-\sqrt{x}{)}^2}(1+x-2\sqrt{x}+y-2\sqrt{y}(1-\sqrt{x})dy$

$V={\int }_0^1[(1+x-2\sqrt{x}).(1-\sqrt{x}{)}^2+\frac{(1-\sqrt{x}{)}^4}{2}-\frac{4}{3}.(1-\sqrt{x}{)}^3(1-\sqrt{x})]dx$

$V=...$ (valeur numérique).

A compléter après avoir tout vérifié, car je n'ai rien relu.

[medou coulibaly]

@Black-Jack Bonjour je trouve V = 1/90

[mtschoon]

@medou-coulibaly , bonjour,
J'ai fait le calcul autrement ( par changement de variables $u=\sqrt{x},v=\sqrt{y},w=\sqrt{z}$ ) et je trouve aussi $\frac{1}{90}$.
Donc, c'est bon.

[medou coulibaly]

@mtschoon Bonjour madame merci beaucoup , j'ai posté un autre exercice j'ai du à démarrer à cause de la valeur absolue