Champ E , Dynamique , centre d’inertie

Bonsoir
On considère un condensateur pian formé par deux plaques verticales P₁ et P₂ de longueur commune = 20 cm, placées à une distance d = 20 cm l'une de l'autre.

On applique une d.d.p. entre P, et P₂ créant ainsi un champ électrique E uniforme, horizontal, dirigé de P₁ vers P₂ et de valeur E = 2 x 104 V/m. On apporte ensuite à l'aide d'un fil isolant non chargé une boule métallisée de masse m = 8 g possédant une charge: q = +3×10-6 C près du bord supérieur de la plaque positive P, en O sans toutefois la toucher.
( svp j’arrive pas à coller l’image dans le furum , et il est un peu compliqué , je ne sais pas si le problème viens de mon téléphone ).

@Zeïnab-Mahamadou regarde sur cette image là où j'ai entouré là, c'est là-bas, tu appuis dessus et tu verras

@medou-coulibaly

Bonjour,

Je présume que le dessin est celui-ci :

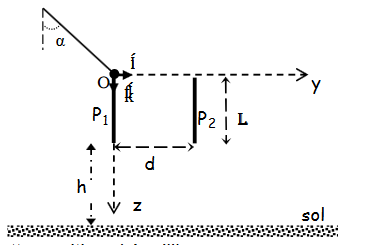
Sans titre.png

Il manque une partie de l'énoncé ...

Et ce que tu as déjà essayé de faire.

@Black-Jack Je pense pas que si votre schéma est différent de son schéma car ( on dit que les deux plaques P1 et P2 sont verticales et après l'effet de la d.d.p et les deux plaques P1 et P2 sont horizontales )
Aussi il manque les questions

@medou-coulibaly a dit dans Champ E , Dynamique , centre d’inertie :

@Black-Jack Je pense pas que si votre schéma est différent de son schéma car ( on dit que les deux plaques P1 et P2 sont verticales et après l'effet de la d.d.p et les deux plaques P1 et P2 sont horizontales )
Aussi il manque les questions

Bonjour,

Il manque effectivement les questions.
Mais il n'y a pas d'incohérence dans la position des plaques.
Les plaques sont verticales.
Et c'est le champ électrique entre les plaques qui est évidemment horizontal.

@medou-coulibaly merci beaucoup, moi j’appuyais sur l’autre , il as fallu tirer la bannière pour voir le reste

Ce message a été supprimé !

@Black-Jack bonsoir

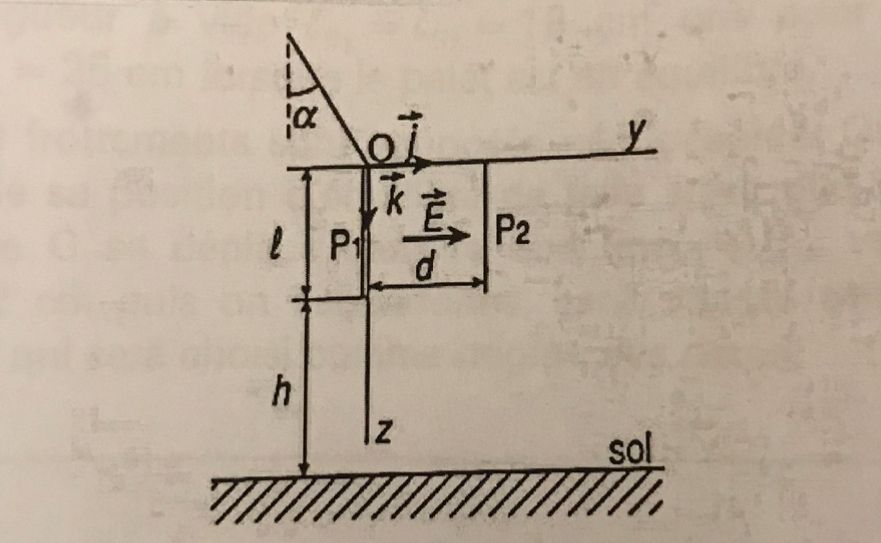
a. Déterminer l'angle alpha que fait le fil avec la verticale dans cette position d'équilibre.

b. On coupe ensuite le fil, libérant ainsi la boule chargée sans vitesse initiale. Indiquer en la justifiant la nature du mouvement de la boule à l'intérieur du condensateur.

Établir les expressions, en fonction du temps y = f(t) et z = f(t). de la trajectoire de la boule dans l'espace plan (O, j, k) limité par les deux plateaux P₁ et P₂. Déduire ensuite l'équation z = f(y) de la trajectoire.

c. Déterminer les coordonnées du point S de sortie de la boule lorsque celle-ci quitte l'espace où agit le champ électrostatique. Calculer la duréet de ce mouvement. Par application d théorème de l'énergie cinétique, déterminer la valeur da vecteur vitesse v, de la boule à cet endroit.

d. Sachant que la partie inférieure de ce condensateur se trouve à une hauteur h = 25 cm du sol, déterminer les coordonnées du point d'impact J de la boule avec le sol et la valeur de son vecteur vitesse v, en ce point.

@Black-Jack
Non j’ai aucune idée de comment début

Bonjour,

a)
Force verticale due à la pesanteur : F1 = m.g = 8.10^-3 * 10 = 8.10^-2 N
Force horizontale due au champ électrique : F2 = E.q = 2.10^4 * 3.10^-6 = 6.10^-2 N

6.10^-2 = 8.10^-2.tan(alpha)
tan(alpha) = 3/4 --> alpha = 36,9° (arrondi)

b)
accélération verticale : g
accélération horizontale : a_h = F2/m = 6.10^-2/(8.10^-3) = 7,5 m/s²

z(t) = gt²/2 = 5.t²
y(t) = a_h*t²/2 = 3,75.t²

z/y = 5/3,75
z = (4/3).y

c)
Lorsque z = L = 0,2 --> y = 3/4 * 0,2 = 0,15 (m), soit 15 cm

S(15;20) (en cm)
S(0,15 ; 0,2) (en m)

z(t) = 5.t²
z(t) = 0,2 = 5t²
t² = 0,04
t = 0,2 s (durée du mouvement)

Vz(t) = 10t
Vy(t) = 7t
Vz(0,2) = 2 m/s
Vy(0,2) = 1,4 m/s
|V| = RacineCarrée(2² + 1,4²) = 2,44 m/s (vitesse en S)

d)
En S, la boule est aux coordonnées (0,15 ; 0,2) (en m)
et les composantes de la vitesse sont :
VS(y) = 1,4 m/s
VS(z) = 2 m/s

Il y a tout ce qu'il faut pour continuer ...

Non sans avoir vérifié et compris ce qui a été fait ... car je n'ai rien relu et donc, erreurs possibles.

@Black-Jack d’accord merci je vais reprendre voir si j’ai compris

@Black-Jack bonsoir
J’ai pas compris la question b)

Rbonjour,

b)

Il y a 2 forces qui agissent sur la boule:

1°) son poids vertical vers le bas (sens des z positifs).
Il y a donc une accélération g dans ce sens et la composante du déplacement suivant cet axe est z(t) = gt²/2 = 5t²

2°) La force due au champ électrique E sur la charge q de la boule, cette force est F2 = Eq, force horizontale dans la direction de l'axe des y.
Il y a donc une accélération horizontale = F2/m = E * q/m
et la composante du déplacement suivant cet axe (des y) est y(t) = (Eq/m)*t²/2 = 2.10^4 * 3.10^-6/(8.10^-3) * t²/2 = 3,75.t²

On a donc :
z(t) = 5t²
y(t) = 3,75t²

On obtient l'équation de la trajectoire en éliminant t entre les 2 équations ci/dessus

z/y = 5t²/(3,75t²)
z/y = 1,3333... (soit 4/3)

--> z = (4/3).y est l'équation de la trajectoire pendant le passage de la boule entre les plaques.

@Black-Jack ok merci

@Black-Jack bonjour
Pour la dernière question
Y= 30cm?
V= 3,33m/s

@Black-Jack a dit dans Champ E , Dynamique , centre d’inertie :

En S, la boule est aux coordonnées (0,15 ; 0,2) (en m)
et les composantes de la vitesse sont :
VS(y) = 1,4 m/s
VS(z) = 2 m/s

Bonjour,

Si on a bien : (ce que je n'ai pas vérifié)
En S, la boule est aux coordonnées (0,15 ; 0,2) (en m)
et les composantes de la vitesse sont :
VS(y) = 1,4 m/s
VS(z) = 2 m/s

Il reste à descendre de h = 0,25 m
Avec l'origine d'horloge prise au passage de la boule par S :
v(Z) = 2 + g.t = 2 + 10t
0,25 = 2t + 10t²/2 = 2t + 5t²
5t² + 2t - 0,25 = 0 ...
t = 0,1 s (durée de la descente)
delta Y = 0,1 * 1,4 = 0,14 m
--> point d'impact en J(0,29 ; 0,45) en m ou bien si on préfère : J(29 ; 45) en cm

Vitesse à l'arrivée au sol :
Vzsol = 2 + 10*0,1 = 3 m/s
Vysol = 1,4 m/s
$\sqrt{3^2 + 1,4^2} = 3,31\ m/s$

Calculs toujours pas vérifiés.