Calcul d'intégrale triple
-
medou coulibaly dernière édition par medou coulibaly

A) calculer ∭ | 𝑥^2 − 𝑦^2 | 𝑑𝑥𝑑𝑦𝑑𝑧 𝑠𝑢𝑟 ∆= { (𝑥, 𝑦, 𝑧) ∈ ℝ³⁺, 𝑥^2 + 𝑦^2 ≤ 𝑧^2 et 0 ≤ 𝑧 ≤ 1}
On pourra utiliser les coordonnées polaires.
-
medou coulibaly dernière édition par

@medou-coulibaly Bonjour comment vous allez, jusque-là j'ai pas reçu d'aide concernant ce poste
-
mtschoon dernière édition par mtschoon

@medou-coulibaly , bonsoir,
Je crois que ton topic a passé inaperçu...
J'espère que tu as terminé cette intégrale.
Si ce n'est pas le cas, je t'indique quelques pistes.Avec le conseil de l'énoncé, utilise les coordonnées polaires.
J=∫∫∣x2−y2∣dxdy\boxed{J=\int\int |x^2-y^2|dxdy}J=∫∫∣x2−y2∣dxdy
x=rcosθx=rcos\thetax=rcosθ
y=rsinθy=rsin\thetay=rsinθ
Tu transformes l'expression de la fonction
∣x2−y2∣=∣r2cos2θ−r2sin2θ∣=r2∣cos2θ−−sin2θ∣|x^2-y^2|=|r^2cos^2\theta-r^2sin^2\theta|=r^2|cos^2\theta--sin^2\theta|∣x2−y2∣=∣r2cos2θ−r2sin2θ∣=r2∣cos2θ−−sin2θ∣
Formule de duplication:
∣x2−y2∣=r2∣cos2θ∣\boxed{|x^2-y^2|=r^2|cos2\theta|}∣x2−y2∣=r2∣cos2θ∣
dxdy=rdrdθ\boxed{dxdy=rdrd\theta}dxdy=rdrdθ
Domaine d'intégration :
𝑥2+𝑦2≤𝑧2𝑥^2 + 𝑦^2 \le 𝑧^2x2+y2≤z2 <=>r2cos2θ+r2sin2θ≤z2r^2cos^2\theta+r^2sin^2\theta\le z^2r2cos2θ+r2sin2θ≤z2
c'est à dire r2(cos2θ+sin2θ)≤z2r^2(cos^2\theta+sin^2\theta)\le z^2r2(cos2θ+sin2θ)≤z2
c'est à dire r2≤z2r^2\le z^2r2≤z2
c'est à dire z≤r\boxed{z\le r}z≤r : disque de centre O et de rayon zzzDonc :
J=∫0zr2rdr∫−ππ∣cos2θ∣dθ\displaystyle J=\int_0^z r^2rdr\int_{-\pi}^{\pi}|cos2\theta|d\thetaJ=∫0zr2rdr∫−ππ∣cos2θ∣dθ
J=∫0zr3dr∫−ππ∣cos2θ∣dθ\displaystyle J=\int_0^z r^3dr\int_{-\pi}^{\pi}|cos2\theta|d\thetaJ=∫0zr3dr∫−ππ∣cos2θ∣dθRemarque : Pour θ\thetaθ, si tu préfères, tu peux prendre l'intervalle [0,2π][0 ,2\pi][0,2π] au lieu de [−π,π][-\pi,\pi][−π,π]. Cela revient au même
J'ai choisi [−π,π][-\pi,\pi][−π,π] pour raison de parité.
-
mtschoon dernière édition par mtschoon

Tu calcules les intégrales
Tu dois trouver après calculs,
∫0zr3dr=.....=z44\displaystyle \int_0^zr^3dr=.....=\dfrac{z^4}{4}∫0zr3dr=.....=4z4Graphique la fonction θ\thetaθ->∣cos2θ∣|cos2\theta|∣cos2θ∣
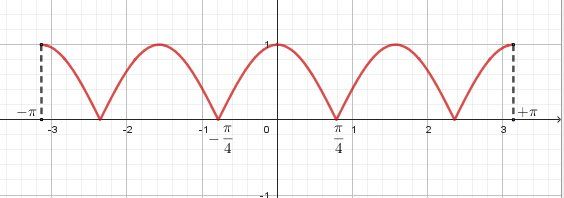
Pour θ∈[0,π4]\theta \in [0,\dfrac{\pi}{4}]θ∈[0,4π], cos2θ≥0cos2\theta\ge 0cos2θ≥0 donc ∣cos2θ∣=cos2θ|cos2\theta|=cos2\theta∣cos2θ∣=cos2θ
Tu peux déduire après calculs,
∫−ππ∣cos2θ∣=8∫0π4cos2θdθ=......=4\displaystyle \int _{-\pi}^{\pi}|cos2\theta|=8\int _0^{\frac{\pi}{4}}cos2\theta d\theta=......=4∫−ππ∣cos2θ∣=8∫04πcos2θdθ=......=4
Ainsi J=(z44)4=z4J=(\dfrac{z^4}{4})4=z^4J=(4z4)4=z4Tu termines en calculant
I=∫∫∫∣x2−y2∣dxdydz=∫01Jdz=∫01z4dzI=\int\int\int |x^2-y^2|dxdydz=\int_0^1Jdz=\int _0^1z^4 dzI=∫∫∫∣x2−y2∣dxdydz=∫01Jdz=∫01z4dzVérifie tout ça et termine
Bons calculs.
-
medou coulibaly dernière édition par

@mtschoon Bonsoir madame j'ai compris et merci beaucoup à vous.Je vais faire les calculs et vous revenir
-
mtschoon dernière édition par

OK @medou-coulibaly .