Princesse, pois et nombre de matelas Formule de BAYES

Aider moi à résoudre ce problème s’il vous plaît
Chaque nuit, une princesse est tout aussi susceptible de dormir sur 6 à 12 matelas. La moitié des nuits de l'année, un pois est placé sous le matelas le plus bas.

• Si le pois est placé sous 6 matelas, il dort bien 0 nuit sur 10. Elle ne dort jamais !
• Si le pois est placé sous 7 matelas, elle dort bien 1 nuit sur 10.
• Si le pois est placé sous 8 matelas, elle dort bien 2 nuits sur 10.
• Si le pois est placé sous 9 matelas, elle dort bien 3 nuits sur 10.
• Si le pois est placé sous 10 matelas, elle dort bien 4 nuits sur 10.
• Si le pois est placé sous 11 matelas, il dort bien 5 nuits sur 10.
• Si le pois est placé sous 12 matelas, elle dort bien 6 nuits sur 10.

Un matin, lorsque son bon ami M. Bayes l'a réveillée, elle a dit qu'elle avait incroyablement bien dormi cette nuit-là !

Quel est le nombre attendu de matelas sur lesquels elle a dormi cette nuit-là ?

Bof,

Je dirais 7 à cause du mot "incroyablement" de l'énoncé.

Mais ceci n'a rien de mathématiques.

Bonjour,

@Idrissa-Sadio , si tu lis bien l'énoncé jusqu'au bout, la marche à suivre est indiquée dans l'énoncé :
Fourmule de BAYES,
Si l'énoncé te parle de M.Bayes, ce n'est pas fortuit...c'est pour te mettre sur la voie...il faut "décoder" !

Si tu ne la connais pas, cette formule, tu peux faire la démarche en deux temps. IL suffit de connaître les probabilités conditionnelles.

@Idrissa-Sadio , il y a une lacune dans ton énoncé.
Tel que tu l'as indiqué, on ne peut pas faire les calculs.

On sait ce qui se passe lorsqu'il y a un pois sous les matelas, mais on ne sait pas ce qui se passe lorsqu'il n'y a pas le pois...
Ou bien tu as oublié d'écrire une ligne, ou bien l'énoncé qui t'a été donné est erroné...

"Traditionnellement", il y aurait dû être indiqué que , lorsqu'il n'y a pas le pois, la princesse dort très bien, quel que soit le nombre de matelas (mais bien sûr, ça pourrait être autre chose !)

Merci de vérifier ton énoncé.

Bonjour,

On ne connait pas non plus les probabilités sur les différents cas avec nombre de matelas différents.
Rien n'indique que dans les nuits avec petits pois, la proba d'avoir 6 ou 7 ou ... 12 matelas est la même.

@mtschoon je crois que c’est cette formule qui me permettra de résoudre cette énigme

@Idrissa-Sadio ,

@Idrissa-Sadio a dit dans Aider moi à résoudre ce problème s’il vous plaît :

@mtschoon je crois que c’est cette formule qui me permettra de résoudre cette énigme

Oui, c'est sûr que c'est la formule de Bayes qui est attendue, à condition d'avoir toutes les indications nécessaires.
On fait au mieux avec les données ...il faut "interpréter", vu que c'est une énigme... !

Je t'indique la démarche que tu peux utiliser, en supposant que, lorsqu'il n'y a pas le pois, la princesse dort très bien.

@Idrissa-Sadio ,
Schéma possible pour clarifier la démarche :

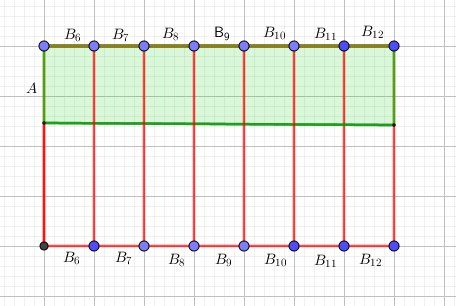
Evènement $A$ "la princesse dort très bien",représenté par la zone verte.
Evènement $B_6$ la princesse dort sur 6 matelas, représentée par la bande verticale entourée de rouge (allant de haut en bas).
Evènement $B_7$ la princesse dort sur 7 matelas, représentée par la bande verticale entourée de rouge (allant de haut en bas).
...
...
Evènement $B_{12}$ la princesse dort sur 12 matelas, représentée par la bande verticale entourée de rouge (allant de haut en bas).

Remarque : j'ai mis les notations des $B_i$ en double pour bien indiquer que les bandes verticales vont de haut en bas.

@Idrissa-Sadio ;

Tu peux décomposer la démarche en deux temps

a) calcul de la probabilité $p (A)$

$A=(A∩B6)∪(A∩B7)∪...∪(A∩B12)A=(A\cap B_6)\cup(A\cap B_7)\cup...\cup(A\cap B_{12})$

$p(A)=p(A∩B6)+p(A∪B7)+...+p(A∩B12)p(A)=p(A\cap B_6)+p(A\cup B_7)+...+p(A\cap B_{12})$

$p(A∩B6)p(A\cap B_6)$ se décompose en deux valeurs :
ou bien la princesse a très bien dormi sur 6 matelas sans le pois (probalité $12\dfrac{1}{2}$ vu que ça se produit la moitié des nuits)
ou bien la princesse a très bien dormi sur 6 matelas avec le pois
probabilité $12×010=0\dfrac{1}{2}\times \dfrac{0}{10}=0$

$p(A∩B6)=12+0=12p(A\cap B_6)=\dfrac{1}{2}+0=\dfrac{1}{2}$

De même,
$p(A∩B7)p(A\cap B_7)$ se décompose en deux valeurs :
ou bien la princesse a très bien dormi sur 7 matelas sans le pois (probalité $12\dfrac{1}{2}$ vu que ça se produit la moitié des nuits)
ou bien la princesse a très bien dormi sur 7 matelas avec le pois
probabilité $12×110=120\dfrac{1}{2}\times \dfrac{1}{10}=\dfrac{1}{20}$

$p(A∩B6)=12+120=1120p(A\cap B_6)=\dfrac{1}{2}+\dfrac{1}{20}=\dfrac{11}{20}$

Tu continues ainsi jusqu'à $p(A∩B12)p(A\cap B_{12})$ et tu ajoutes le tout pour avoir $p (A)$

@Idrissa-Sadio

b) calcul des $p_A{(B_i)}$ ,c'est à dire probabilité que la princesse ait dormi sur $i$ matelas, sachant qu'elle a très bien dormi , pour $i$ allant de 6 à 12.
On appelle cela parfois la "probabilité des causes"

$pA(B6)=p(A∩B6)p(A)=12p(A)p_A(B_6)=\dfrac{p(A\cap B_6)}{p(A)}=\dfrac{\dfrac{1}{2}}{p(A)}$

Tu remplaces $p (A)$ par la valeur trouvée à la partie a)

$pA(B7)=p(A∩B7)p(A)=1120p(A)p_A(B_7)=\dfrac{p(A\cap B_7)}{p(A)}=\dfrac{\dfrac{11}{20}}{p(A)}$

Tu remplaces $p (A)$ par la valeur trouvée à la partie a)

Tu continues ainsi jusqu'à $p_A(B_{12}$ )

Tu pourras conclure en donnant le nombre de matelas correspondant à la plus grande probabilité conditionnelle ainsi trouvée.
Ce sera la valeur "la plus probable".

@mtschoon je pense que ton idée marche je vais me concentrer sur ça et voir ce que cela va donner

Bonnes réflexions @Idrissa-Sadio

Sur le web, je viens de trouver un énoncé (sans la correction) d'un exercice de ENS 2015.

C'est du même type que le tien, mais la rédaction est plus rigoureuse.

Je te le mets pour consultation éventuelle.

@mtschoon en suivant vos consignes j’ai trouvé que est le nombre attendu de matelas sur lesquels elle a dormi cette nuit-là est de 8 matelas

@mtschoon est je que je peux avoir votre mail pour vous envoyer le document?

@mtschoon

Bonjour,

L'énoncé de ton lien est complet.

Celui donné dans le post initial ne l'est pas du tout et rend le problème inepte.

La première phrase du lien est :

Chaque nuit, le prince choisit au hasard de dormir sur 6,7 ou bien 8 matelas (avec des probabilités égales).

Sans une phrase équivalente dans l'énoncé, celui-ci devient inepte ... comme je l'avais fait remarquer dans un message précédent par "On ne connait pas non plus les probabilités sur les différents cas avec nombre de matelas différents.
Rien n'indique que dans les nuits avec petits pois, la proba d'avoir 6 ou 7 ou ... 12 matelas est la même."

Il y a encore d'autres inepties dans l'énoncé donné ici.
Ne serait-ce que la manière dont la question finale est posée, à comparer à celle du lien qui elle est sensée.

Oui @Black-Jack , l'énoncé de @Idrissa-Sadio laisse à désirer...celui que j'ai mis en lien est rigoureux.

@Idrissa-Sadio a dit dans Princesse, pois et nombre de matelas Formule de BAYES :

@mtschoon est je que je peux avoir votre mail pour vous envoyer le document?

@Idrissa-Sadio , ça ne se fait pas...
Ici, on écrit l'énoncé et les réponses éventuelles dans le cadre texte pour que tous les consultants puissent les voir pour progresser dans leur travail.

@mtschoon j’ai suivi la démarche indiquée en calculant les probabilités de chaque événement pour obtenir P(A) puis puis j’ai calculé la probabilité de A sachant B_i pour déterminer. Ainsi pour déterminer le nombre attendu de matelas sur lesquels elle dit avoir incroyablement bien dormi j’ai choisi la probabilité qui a la plus haute valeur qui correspond au matelas 8

@mtschoon ![text alternatif]( url de l'image)

@Idrissa-Sadio ![text alternatif]( url de l'image) la suite

@Idrissa-Sadio , re-bonjour,

Je n'ai pas vérifié tes calculs, mais vu que l'ordre des valeurs indiquées pour "bien dormir" est croissant, c'est normal que la valeur à donner soit 12.

Tu n'y peux rien, mais ton énoncé n'est guère pertinent...

L'essentiel bien sûr est que tu ai compris la méthode ( qui peut s'appliquer dans de nombreux exercices ).

Bon travail !

@mtschoon c’est 8 aulieu de 12 j’ai fait une erreur

@Idrissa-Sadio , vérifir ton calcul pour $p(A∩B8)p(A\cap B_8)$

$12+110=610\dfrac{1}{2}+\dfrac{1}{10}=\dfrac{6}{10}$

@Idrissa-Sadio , bonsoir,
J'espère que tu as compris ta faute de calcul pour $8$ et que tu as tiré la conclusion que la réponse est bien $12$

Bonjour
Oui j’ai tout rectifié
Merci pour les explications et l’aide.

De rien @Idrissa-Sadio et bon travail.