Exercice de trigonometrie

[jary]

Bonjour, j'aurais besoin de vos lumières concernant un exercice dont la solution donnée en classe me semble erronée.
Un jeune homme mesure un angle de 48 degrés entre lui et une tour.
Il recule de 50 mètres et remesure un nouvel angle de 40 degrés.
Quelle est la hauteur de la tour?

[mtschoon]

@jary , bonsoir,

Vu que la solution t'a été donnée en classe, indique nous les principes de la solution et ce qui te pose problème.
Nous te nous te donnerons notre avis.

Idée :
Faire un schéma pour clarifier la situation
Utiliser les tangentes de 48° et 40°

[jary]

@mtschoon
Merci à toi.
C'est mon neveu qui a du résoudre ce problème et non moi.
Triangle ABC angle de 40 degrés en A
Triangle DBC angle de 48 degrés en D
AD = 50 donc AC = DC + 50
La question est quelle est la mesure de BC en utilisant les tangentes?
Merci.

[jary]

@jary
En classe le professeur à donné DC = 133 mètres je ne sais par quel calcul.
En utilisant les tangentes sur les 2 triangles pour vérifier la longueur de BC les 2 résultats ne correspondent pas, d'où mon questionnement.

[mtschoon]

@jary

J'espère avoir utilisé tes notations

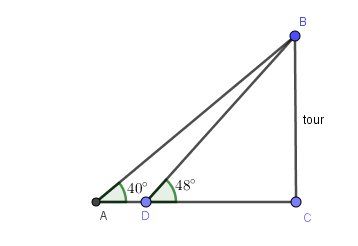
Pistes,

tan48°=$\frac{BC}{DC}$

tan40°=$\frac{BC}{50+DC}$

Donc:

$DC\times tan48°=(50+DC)\times tan40°$

Tu peux trouver $DC$ avec cette égalité.

Puis, la hauteur de la tour est $BC=DC\times tan48°$

Bons calculs.

Une valeur approchée de la tour doit être $171.615$ mètres

[jary]

@mtschoon

Bonjour @mtschoon ,
Je te remercie infiniment pour le temps que tu m'a consacré.
Le jour où j'ai fais moi-même le calcul, mon résultat approximatif était de 171,82 mètres.
Ton résultat rejoint donc le mien et me prouve que j'ai raison depuis le début.
J'espère que mon neveu osera faire reprendre cet exercice à son professeur.

Je te suis très reconnaissant pour ton aide.
Merci à toi.

[mtschoon]

@jary ,

Si ça t'arrange, je t'indique les expressions détaillées que tu dois (ou a dû) trouver :

$DC=\frac{50\times tan(40°)}{tan(48°)-tan(40°)}$

$DC\approx 154.523$

Remarque : Ce n'est pas heureux d'utiliser cette valeur approchée pour la suite du calcul ; il vaut toujours mieux utiliser la valeur exacte pour poursuivre les calculs et ne chercher une valeur approchée qu'à la toute fin.

$BC=\left(\frac{50\times tan(40°)}{tan(48°)-tan(40°)}\right)\times tan(48°)$

$BC\approx 171,615$

[jary]

@mtschoon
Tu es au top
Merci beaucoup

[mtschoon]

De rien @jary
Si maintenent tout est clair pour toi, c'est parfait!