Exercice Pythagore et parrallelisme

Bonjour
J aurai besoin d aide pour me corriger sur un exercice
Merci d avance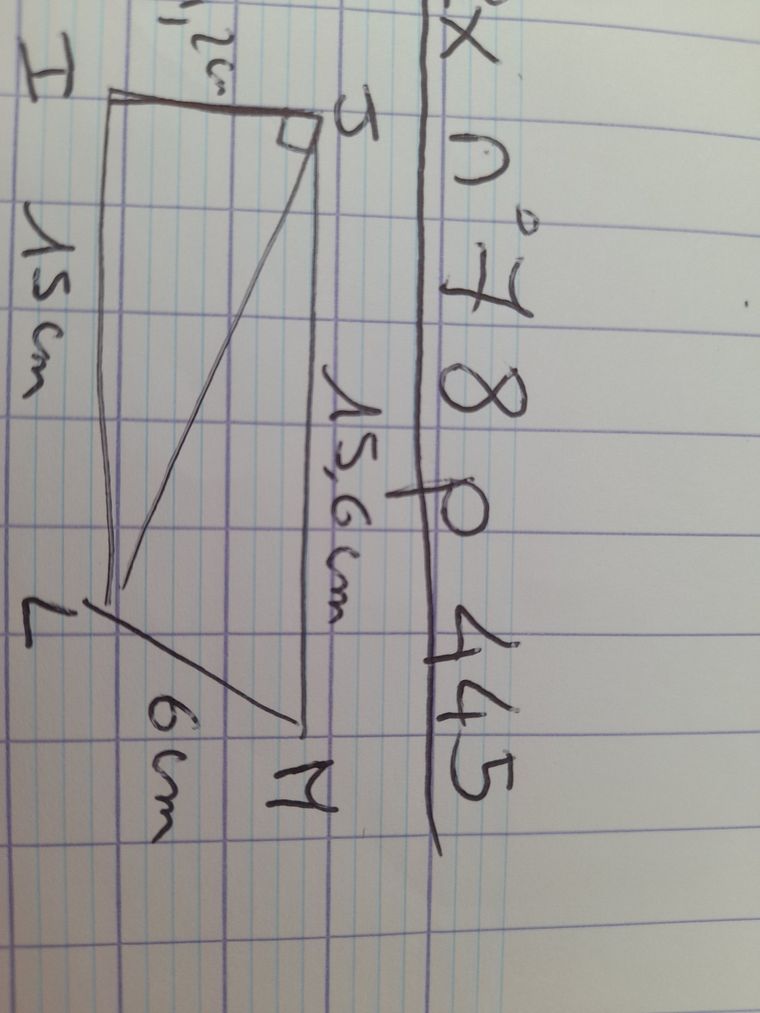

Les mesures ji 4.2 , il 15 , je 15.6 , lm 6

A calculer la longueur de la diagonale JL du quadri ILMJ

j hésite entre 2 formules
JL AU CARRE = IJ AU CARRE +IL AU CARRE

OU IL AU CARRE = JL AU CARRE + ji au carre

@m12 , bonjour,

IL semble, sur ton schéma, que le triangle $I J L$ est rectangle en $I$
Si c'est bien ça, l'hypoténuse est [JL]

Le théorème de Pythagore te permet d'écrire :
$JL^2=IJ^2+IL^2$

Bonjour,

Je mettrais vos tête à couper qu'un dessin convenable est :

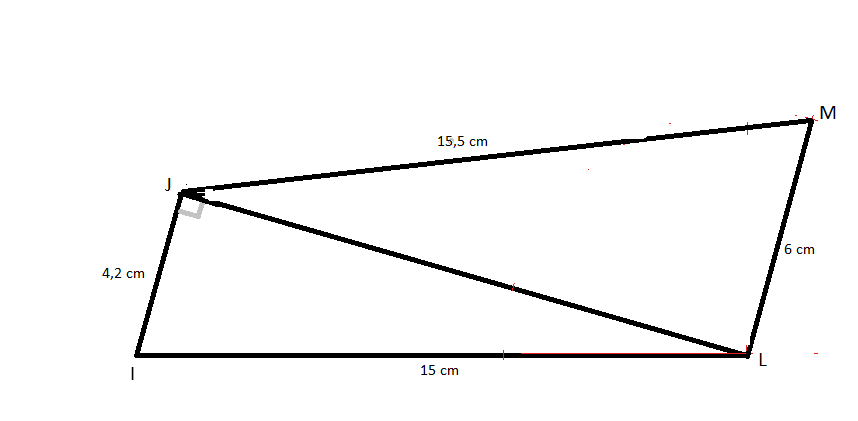
Sans titre.png

@mtschoon a dit dans Exercice Pythagore et parrallelisme :

@m12 , bonjour,

IL semble, sur ton schéma, que le triangle $I J L$ est rectangle en $I$
Si c'est bien ça, l'hypoténuse est [JL]

Le théorème de Pythagore te permet d'écrire :
$JL^2=IJ^2+IL^2$

Non rectangle en J

@Black-Jack a dit dans Exercice Pythagore et parrallelisme :

Bonjour,

Je mettrais vos tête à couper qu'un dessin convenable est :

Oui c est ça sauf 15.6 pour jm

Bonsoir,

@m12 , il aurait été heureux de faire un dessin correct !

Si le triangle $I J L$ est rectangle en $J$ , l' hypoténuse est $I L$

Le théorème de Pythagore te permet d'écrire :

$IL^2=IJ^2+JL^2$

Si c'est $J L$ que tu cherches :

$JL^2=IL^2-IJ^2$

Tu remplaces $I L$ et $J L$ par leurs valeurs et tu comptes

@mtschoon a dit dans Exercice Pythagore et parrallelisme :

Bonsoir,

@m12 , il aurait été heureux de faire un dessin correct !

Si le triangle $I J L$ est rectangle en $J$ , l' hypoténuse est $I L$

Le théorème de Pythagore te permet d'écrire :

$IL^2=IJ^2+JL^2$

Si c'est $J L$ que tu cherches :

$JL^2=IL^2-IJ^2$

Tu remplaces $I L$ et $J L$ par leurs valeurs et tu comptes

C'est bien ce que je pensais
JL AU CARRE= JI AU CARRE + IL AU CARRE
JL AU CARRE = 4.2 AU CARRE + 15 AU CARRE
JL AU CARRE = 17.64 + 225
JL AU CARRE = 242.62
RACINE CARRE DE 241.62

@m12 a dit dans Exercice Pythagore et parrallelisme :

@mtschoon a dit dans Exercice Pythagore et parrallelisme :

Bonsoir,

@m12 , il aurait été heureux de faire un dessin correct !

Si le triangle $I J L$ est rectangle en $J$ , l' hypoténuse est $I L$

Le théorème de Pythagore te permet d'écrire :

$IL^2=IJ^2+JL^2$

Si c'est $J L$ que tu cherches :

$JL^2=IL^2-IJ^2$

Tu remplaces $I L$ et $J L$ par leurs valeurs et tu comptes

C'est bien ce que je pensais
JL AU CARRE= JI AU CARRE + IL AU CARRE
JL AU CARRE = 4.2 AU CARRE + 15 AU CARRE
JL AU CARRE = 17.64 + 225
JL AU CARRE = 242.62
RACINE CARRE DE 241.62

Je le suis tromper
Jl = 15 zu CARRE - 4.2 au carré
JL = 14.40 cm

C'est ça?

@m12 ,

Tu confonds $J L$ avec $JL^2$ dans tes écritures

$JL^2=IL^2-IJ^2$

Avec $I L = 15$ et $I J = 4.2$ (en cm), tu obtiens :

$JL^2=15^2-4.2^2$

Tu dois obtenir $JL^2=207.36$

D'où $JL=207.36JL=\sqrt{207.36}$ (en cm)

A la calculette , on trouve bien : $J L = 14.4$ (en cm)

@mtschoon a dit dans Exercice Pythagore et parrallelisme :

@m12 ,

Tu confonds $J L$ avec $JL^2$ dans tes écritures

$JL^2=IL^2-IJ^2$

Avec $I L = 15$ et $I J = 4.2$ (en cm), tu obtiens :

$JL^2=15^2-4.2^2$

Tu dois obtenir $JL^2=207.36$

D'où $JL=207.36JL=\sqrt{207.36}$ (en cm)

A la calculette , on trouve bien : $J L = 14.4$ (en cm)

Oui c'est vrai
Merci

@mtschoon a dit dans Exercice Pythagore et parrallelisme :

@m12 ,

Tu confonds $J L$ avec $JL^2$ dans tes écritures

$JL^2=IL^2-IJ^2$

Avec $I L = 15$ et $I J = 4.2$ (en cm), tu obtiens :

$JL^2=15^2-4.2^2$

Tu dois obtenir $JL^2=207.36$

D'où $JL=207.36JL=\sqrt{207.36}$ (en cm)

A la calculette , on trouve bien : $J L = 14.4$ (en cm)

Deuxième question

Prouver que le triangle jlm est rectangle

J ai utilisé la réciproque de Pythagore
JM2= 15.6 AU CARRE = 243.36

Jl2 + Lm2 = 14.40 au carré + 6 au carré = 243.36

Donc Jlm est rectangle en L
Est ce cela ?

Oui @m12 , ta seconde question est bonne.

Bonjour,

Zut alors, voila le dessin corrigé.

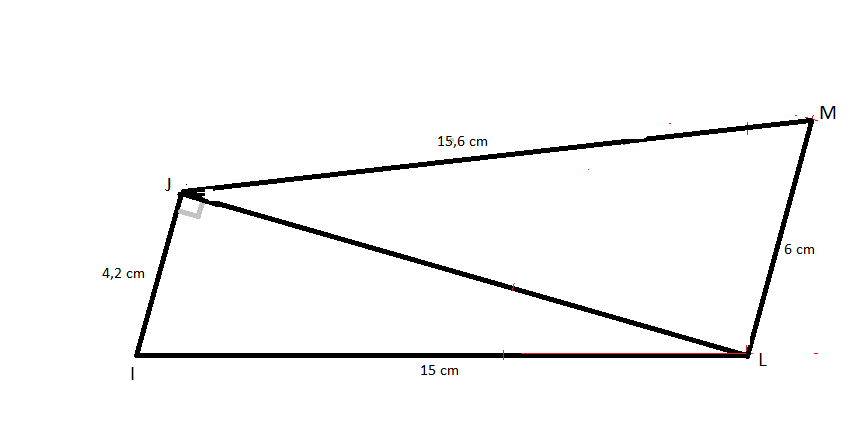
Sans titre.png

@mtschoon a dit dans Exercice Pythagore et parrallelisme :

Oui @m12 , ta seconde question est bonne.

Merci

De rien @m12 et bon travail.