Problème trajet du robot
-
Mm12 dernière édition par
Parti du point D du segment ab tel que bd =2 cm un robot se déplace parallèlement aux côtes du triangle abc
Le robot va t il repasser par D
Et la distance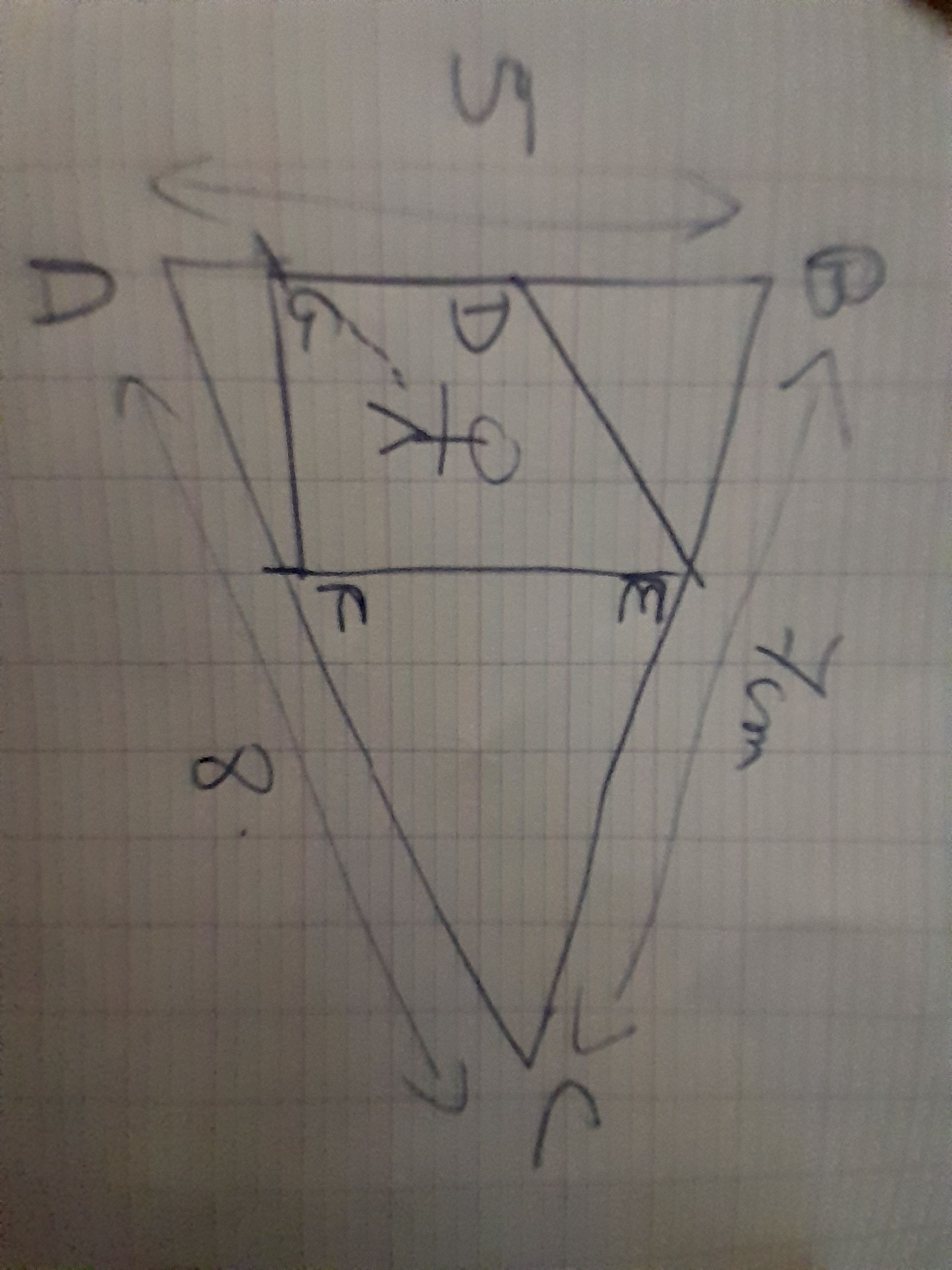
-
Mm12 dernière édition par
@m12 a dit dans Problème trajet du robot :
Parti du point D du segment ab tel que bd =2 cm un robot se déplace parallèlement aux côtes du triangle abc
Le robot va t il repasser par D
Et la distance
J ai commencé par chercher BE
J ai trouver 2.8 cm
-
Mm12 dernière édition par
@m12 a dit dans Problème trajet du robot :
@m12 a dit dans Problème trajet du robot :
Parti du point D du segment ab tel que bd =2 cm un robot se déplace parallèlement aux côtes du triangle abc
Le robot va t il repasser par D
Et la distance
J ai commencé par chercher BE
J ai trouver 2.8 cmPouvez vous m aider sur celui la svp merci
-
BBlack-Jack dernière édition par Black-Jack
@m12 a dit dans Problème trajet du robot :
J ai commencé par chercher BE
J ai trouver 2.8 cmBonjour,
"J ai commencé par chercher BE
J ai trouver 2.8 cm"C'est juste (à la faute d'orthographe près)
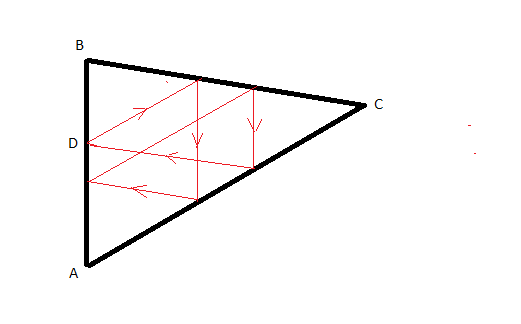
Calcule quelques autres longueurs et ...
-
BBlack-Jack dernière édition par
Ce message a été supprimé !
-
Mm12 dernière édition par
@Black-Jack a dit dans Problème trajet du robot :
@m12 a dit dans Problème trajet du robot :
J ai commencé par chercher BE
J ai trouver 2.8 cmBonjour,
"J ai commencé par chercher BE
J ai trouver 2.8 cm"C'est juste (à la faute d'orthographe près)
Calcule quelques autres longueurs et ...

DG = 5-2 = 3CM
-
Mm12 dernière édition par
@m12 a dit dans Problème trajet du robot :
@Black-Jack a dit dans Problème trajet du robot :
@m12 a dit dans Problème trajet du robot :
J ai commencé par chercher BE
J ai trouver 2.8 cmBonjour,
"J ai commencé par chercher BE
J ai trouver 2.8 cm"C'est juste (à la faute d'orthographe près)
Calcule quelques autres longueurs et ...

DG = 5-2 = 3CM
Je le suis trompé
AD = 5-3 = 3 CMET AF= 4.8 cm AF/AC = AD/AB Af/8= 3/5 = 4.8
-
Mm12 dernière édition par
@m12 a dit dans Problème trajet du robot :
@m12 a dit dans Problème trajet du robot :
@Black-Jack a dit dans Problème trajet du robot :
@m12 a dit dans Problème trajet du robot :
J ai commencé par chercher BE
J ai trouver 2.8 cmBonjour,
"J ai commencé par chercher BE
J ai trouver 2.8 cm"C'est juste (à la faute d'orthographe près)
Calcule quelques autres longueurs et ...

DG = 5-2 = 3CM
Je le suis trompé
AD = 5-3 = 3 CMET AF= 4.8 cm AF/AC = AD/AB Af/8= 3/5 = 4.8
EC= 7-2.8 = 4.2 CM
FC= 8-4,8 = 3.2 CMC est bon?
-
BBlack-Jack dernière édition par
Bonjour,
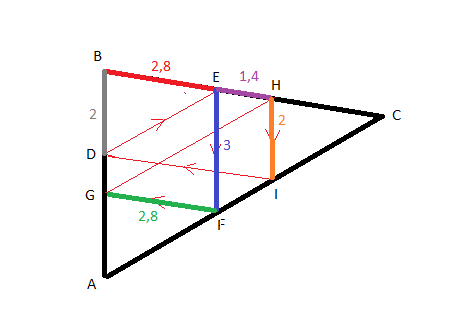
Plusieurs approches sont possibles :
En voila une avec les résultats des calculs faits (en différentes couleurs).On fini par trouver HI = 2 cm et comme BD et HI sont parallèles, le quadrilatère BHID est un parallélogramme ... et le voyage du robot repasse donc par D.
-
Mm12 dernière édition par
@Black-Jack a dit dans Problème trajet du robot :
Bonjour,
Plusieurs approches sont possibles :
En voila une avec les résultats des calculs faits (en différentes couleurs).On fini par trouver HI = 2 cm et comme BD et HI sont parallèles, le quadrilatère BHID est un parallélogramme ... et le voyage du robot repasse donc par D.

Je sais pas comment trouver DE, EF , GF et DG
-
BBlack-Jack dernière édition par Black-Jack
Rebonjour,
Par exemple :
Les triangles BDE et BAC sont semblables (de même forme) --> BE/BC = DE/AC
DE = (BE*AC)/BC = 2,8 * 8/7 = 3,2 (cm)
Les triangles EFC et BAC sont semblables (de même forme) --> EF/BA = EC/BC
EF = (BA * EC)/BC
EF = (BA * (BC - BE))/BC
EF = (5 * (7 - 2,8))/7 = 3 (cm)
Raisonnements analogues pour les autres longueurs ... en se servant des propriétés des triangles semblables
-
Mm12 dernière édition par
@Black-Jack a dit dans Problème trajet du robot :
Rebonjour,
Par exemple :
Les triangles BDE et BAC sont semblables (de même forme) --> BE/BC = DE/AC
DE = (BE*AC)/BC = 2,8 * 8/7 = 3,2 (cm)
Les triangles EFC et BAC sont semblables (de même forme) --> EF/BA = EC/BC
EF = (BA * EC)/BC
EF = (BA * (BC - BE))/BC
EF = (5 * (7 - 2,8))/7 = 3 (cm)
Raisonnements analogues pour les autres longueurs ... en se servant des propriétés des triangles semblables
Pour les triangles EFC et BAC je trouve Ef = 2 cm
EF/BA= FC/AC=EC/BcnC
EF/5=3,2/8=4,2/7
EF= 5X3.2/8 = 2 cmPour l autre je trouve pareil
-
BBlack-Jack dernière édition par
@m12 a dit dans Problème trajet du robot :
@Black-Jack a dit dans Problème trajet du robot :
Rebonjour,
Par exemple :
Les triangles BDE et BAC sont semblables (de même forme) --> BE/BC = DE/AC
DE = (BE*AC)/BC = 2,8 * 8/7 = 3,2 (cm)
Les triangles EFC et BAC sont semblables (de même forme) --> EF/BA = EC/BC
EF = (BA * EC)/BC
EF = (BA * (BC - BE))/BC
EF = (5 * (7 - 2,8))/7 = 3 (cm)
Raisonnements analogues pour les autres longueurs ... en se servant des propriétés des triangles semblables
Pour les triangles EFC et BAC je trouve Ef = 2 cm
EF/BA= FC/AC=EC/BcnC
EF/5=3,2/8=4,2/7
EF= 5X3.2/8 = 2 cmPour l autre je trouve pareil
C'est faux. J'ai fait le calcul (voir ma réponse précédente) et on trouve EF = 3 cm
Tu écris :
EF/BA= FC/AC=EC/BC ... cà c'est OK
Mais FC n'est pas égal à 3,2 comme tu l'écris.
Par contre ton EF/5 = 4,2/7 est juste ...
Mais cela donne bien EF = 5 * 4,2/7 = 3 cm
-
Mm12 dernière édition par
@Black-Jack a dit dans Problème trajet du robot :
@m12 a dit dans Problème trajet du robot :
@Black-Jack a dit dans Problème trajet du robot :
Rebonjour,
Par exemple :
Les triangles BDE et BAC sont semblables (de même forme) --> BE/BC = DE/AC
DE = (BE*AC)/BC = 2,8 * 8/7 = 3,2 (cm)
Les triangles EFC et BAC sont semblables (de même forme) --> EF/BA = EC/BC
EF = (BA * EC)/BC
EF = (BA * (BC - BE))/BC
EF = (5 * (7 - 2,8))/7 = 3 (cm)
Raisonnements analogues pour les autres longueurs ... en se servant des propriétés des triangles semblables
Pour les triangles EFC et BAC je trouve Ef = 2 cm
EF/BA= FC/AC=EC/BcnC
EF/5=3,2/8=4,2/7
EF= 5X3.2/8 = 2 cmPour l autre je trouve pareil
C'est faux. J'ai fait le calcul (voir ma réponse précédente) et on trouve EF = 3 cm
Tu écris :
EF/BA= FC/AC=EC/BC ... cà c'est OK
Mais FC n'est pas égal à 3,2 comme tu l'écris.
Par contre ton EF/5 = 4,2/7 est juste ...
Mais cela donne bien EF = 5 * 4,2/7 = 3 cmPour AF je trouve AF/Ac= AD/AB
AF/8= 3/5
AF= 8x3/5
AF= 4.8
-
Mm12 dernière édition par
@Black-Jack a dit dans Problème trajet du robot :
@m12 a dit dans Problème trajet du robot :
@Black-Jack a dit dans Problème trajet du robot :
Rebonjour,
Par exemple :
Les triangles BDE et BAC sont semblables (de même forme) --> BE/BC = DE/AC
DE = (BE*AC)/BC = 2,8 * 8/7 = 3,2 (cm)
Les triangles EFC et BAC sont semblables (de même forme) --> EF/BA = EC/BC
EF = (BA * EC)/BC
EF = (BA * (BC - BE))/BC
EF = (5 * (7 - 2,8))/7 = 3 (cm)
Raisonnements analogues pour les autres longueurs ... en se servant des propriétés des triangles semblables
Pour les triangles EFC et BAC je trouve Ef = 2 cm
EF/BA= FC/AC=EC/BcnC
EF/5=3,2/8=4,2/7
EF= 5X3.2/8 = 2 cmPour l autre je trouve pareil
C'est faux. J'ai fait le calcul (voir ma réponse précédente) et on trouve EF = 3 cm
Tu écris :
EF/BA= FC/AC=EC/BC ... cà c'est OK
Mais FC n'est pas égal à 3,2 comme tu l'écris.
Par contre ton EF/5 = 4,2/7 est juste ...
Mais cela donne bien EF = 5 * 4,2/7 = 3 cmDu coup FC fait combien
Car moi j ai fais Ac- af
-
Mm12 dernière édition par
@Black-Jack a dit dans Problème trajet du robot :
@m12 a dit dans Problème trajet du robot :
@Black-Jack a dit dans Problème trajet du robot :
Rebonjour,
Par exemple :
Les triangles BDE et BAC sont semblables (de même forme) --> BE/BC = DE/AC
DE = (BE*AC)/BC = 2,8 * 8/7 = 3,2 (cm)
Les triangles EFC et BAC sont semblables (de même forme) --> EF/BA = EC/BC
EF = (BA * EC)/BC
EF = (BA * (BC - BE))/BC
EF = (5 * (7 - 2,8))/7 = 3 (cm)
Raisonnements analogues pour les autres longueurs ... en se servant des propriétés des triangles semblables
Pour les triangles EFC et BAC je trouve Ef = 2 cm
EF/BA= FC/AC=EC/BcnC
EF/5=3,2/8=4,2/7
EF= 5X3.2/8 = 2 cmPour l autre je trouve pareil
C'est faux. J'ai fait le calcul (voir ma réponse précédente) et on trouve EF = 3 cm
Tu écris :
EF/BA= FC/AC=EC/BC ... cà c'est OK
Mais FC n'est pas égal à 3,2 comme tu l'écris.
Par contre ton EF/5 = 4,2/7 est juste ...
Mais cela donne bien EF = 5 * 4,2/7 = 3 cmComment on trouve GH et H i du coup,
-
BBlack-Jack dernière édition par
Bonjour,
Par exemple (il y a diverses manières d'y arriver) :
BE est parallèle GF et BG est parallèle à EF --> BEFG est un parallélogramme
Et donc GF = BE
--> GF = 2,8 (cm)Les triangles GFA et BCA sont semblables --> GF/BC = GA/AB
2,8/7 = GA/5
GA = 2,8*5/7 = 2 (cm)BG = BA-GA
BG = 5-2 = 3 (cm)Les triangles BGH et BAC sont semblables --> GH/AC = BG/BA = BH/BC
GH/8 = 3/5 = BH/7
--> GH = 4,8 (cm) et BH = 4,2 (cm)HC = BC - BH = 7 - 4,2 = 2,8 (cm)
Les triangles HCI et BCA sont semblables --> HI/BA = HC/BC
HI/5 = 2,8/7
HI = 5*2,8/7 = 2 (cm)
-
Mm12 dernière édition par
@Black-Jack a dit dans Problème trajet du robot :
@m12 a dit dans Problème trajet du robot :
@Black-Jack a dit dans Problème trajet du robot :
Rebonjour,
Par exemple :
Les triangles BDE et BAC sont semblables (de même forme) --> BE/BC = DE/AC
DE = (BE*AC)/BC = 2,8 * 8/7 = 3,2 (cm)
Les triangles EFC et BAC sont semblables (de même forme) --> EF/BA = EC/BC
EF = (BA * EC)/BC
EF = (BA * (BC - BE))/BC
EF = (5 * (7 - 2,8))/7 = 3 (cm)
Raisonnements analogues pour les autres longueurs ... en se servant des propriétés des triangles semblables
Pour les triangles EFC et BAC je trouve Ef = 2 cm
EF/BA= FC/AC=EC/BcnC
EF/5=3,2/8=4,2/7
EF= 5X3.2/8 = 2 cmPour l autre je trouve pareil
C'est faux. J'ai fait le calcul (voir ma réponse précédente) et on trouve EF = 3 cm
Tu écris :
EF/BA= FC/AC=EC/BC ... cà c'est OK
Mais FC n'est pas égal à 3,2 comme tu l'écris.
Par contre ton EF/5 = 4,2/7 est juste ...
Mais cela donne bien EF = 5 * 4,2/7 = 3 cmBonjour Pouvez vous m aider j arrive pas à trouver GH
-
Mm12 dernière édition par
@Black-Jack a dit dans Problème trajet du robot :
Bonjour,
Par exemple (il y a diverses manières d'y arriver) :
BE est parallèle GF et BG est parallèle à EF --> BEFG est un parallélogramme
Et donc GF = BE
--> GF = 2,8 (cm)Les triangles GFA et BCA sont semblables --> GF/BC = GA/AB
2,8/7 = GA/5
GA = 2,8*5/7 = 2 (cm)BG = BA-GA
BG = 5-2 = 3 (cm)Les triangles BGH et BAC sont semblables --> GH/AC = BG/BA = BH/BC
GH/8 = 3/5 = BH/7
--> GH = 4,8 (cm) et BH = 4,2 (cm)HC = BC - BH = 7 - 4,2 = 2,8 (cm)
Les triangles HCI et BCA sont semblables --> HI/BA = HC/BC
HI/5 = 2,8/7
HI = 5*2,8/7 = 2 (cm)Merci
-
Mm12 dernière édition par
@m12 a dit dans Problème trajet du robot :
@Black-Jack a dit dans Problème trajet du robot :
Bonjour,
Par exemple (il y a diverses manières d'y arriver) :
BE est parallèle GF et BG est parallèle à EF --> BEFG est un parallélogramme
Et donc GF = BE
--> GF = 2,8 (cm)Les triangles GFA et BCA sont semblables --> GF/BC = GA/AB
2,8/7 = GA/5
GA = 2,8*5/7 = 2 (cm)BG = BA-GA
BG = 5-2 = 3 (cm)Les triangles BGH et BAC sont semblables --> GH/AC = BG/BA = BH/BC
GH/8 = 3/5 = BH/7
--> GH = 4,8 (cm) et BH = 4,2 (cm)HC = BC - BH = 7 - 4,2 = 2,8 (cm)
Les triangles HCI et BCA sont semblables --> HI/BA = HC/BC
HI/5 = 2,8/7
HI = 5*2,8/7 = 2 (cm)Merci
Lr trajet total fait 20 cm