DM de mécanique des solides

Bonjour j'espère que vous allez bien , j'ai besoin d'aide pour mon DM que je ne trouve pas d'issue.
Une barre mince de masse m et de longueur L est fixée à un arbre vertical qui tourne à une vitesse angulaire constante Ω , comme le montre la figure 3.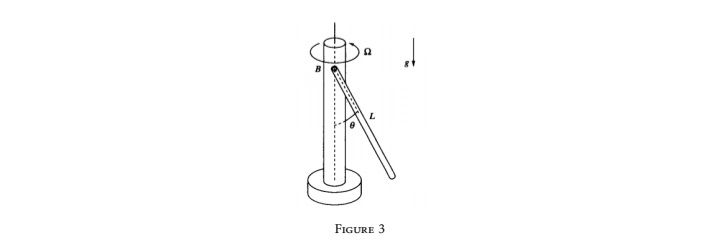
Déterminer l'équation du mouvement de la barre.

@medou-coulibaly Bonjour jusque-là je ne trouve pas de solution face à mon exercice

Bonjour,

La question n'est pas explicite.

Demande-t-on de définir le mouvement lorsqu'il est stabilisé ou bien la phase transitoire qui fait passer la tige d'une position initiale verticale (par exemple) à sa position finale ?

Quand le mouvement est stabilisé, la tige tourne (voir dessin) en faisant un angle theta (constant dans le temps) avec l'arbre.

Calcul de cet angle theta ...

J(tige) = mL²/3
E cinétique de la tige = 1/2.J.w² = mL²w²/6

Variation d'énergie potentielle depuis la position de départ (le centre d'inertie de loa tige "monte" de Delta h = L/2 * (1-cos(theta))
Delta Ep = m.g. L/2 * (1-cos(theta))

On a donc : mL²w²/6 =m.g. L/2 * (1-cos(theta))
Lw²/(3g) = 1-cos(theta)
cos(theta) = 1 - (w²L/(3g))

$θ=arccos(1−ω2.L3g)\theta = arccos(1 - \frac{\omega^2.L}{3g} )$

Toutes distractions incluses.

@Black-Jack bonsoir monsieur merci beaucoup à vous