Train d’engrenages asymétrique

[JLF]

Bonjour,

Préoccupé par les enjeux environnementaux et énergétiques auxquels le monde est confronté ; j’étudie actuellement un train d’engrenages asymétrique ; qui permettrait la levée des charges avec la facilité d’un contrepoids, mais sans contrepoids.
Des économies d’énergie seraient réalisables si mon hypothèse était validée par la pratique .

Je souhaiterais savoir si mon raisonnement est correct.
Les textes et images son ma création, donc aucun souci pour les références ou droits d’auteurs.
Par avance merci de prendre de votre temps à lire la totalité du sujet.
Train d’engrenages asymétrique :
Caractéristiques : Module 2
Couronnes Planétaires 60 dents Ø 120 mm
Pignons satellites 20 dents Ø 40 mm
Pignons planétaires 20 dents Ø 40 mm
Étude pour 4 tours des pignons planétaires soit 25,12 radiant (rad).
Les pertes mécaniques moyennes dans un engrenage épicycloïdal sont égales à 2,5 %

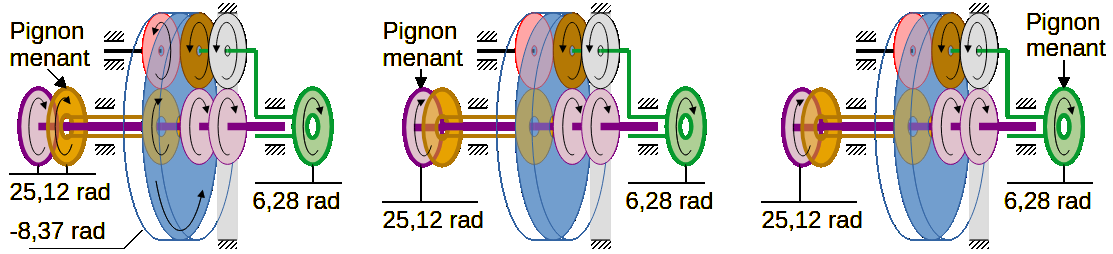
Important
Des couples égaux et opposés, sur les pignons planétaires seraient donc équilibrés. Ils seraient incapables d’influencer la motricité sur le porte-satellites vert, qui n’assumerait que les pertes mécaniques, pour faire tourner le pignon planétaire mauve.
Ce train d’engrenages n’est pas un différentiel classique. Les pignons planétaires orange et mauve, ne peuvent pas tourner en sens inverse, simultanément l’un par rapport à l’autre.
L’équilibre en (A) ou (B) rend impossible le cas (C).

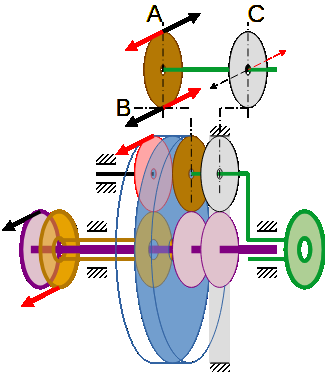
Calculs des puissances pour des couples égaux et opposés de 100 Nm sur les pignons planétaires :
En équilibre : en (A) ou (B) => 100 – 100 = 0 Nm
En rotation : entraîné par le porte-satellites vert à 6,28 rad/s
_ Rotation du pignon satellite marron : (25,12 – 6,28) = 18,84 rad/s => 133 N/m
_ Tentative de rotation de la couronne bleue : (25,15/3) = 8,37 rad/s => 300 N/m
Rotation de l’engrènement de (A) : (8,37x300) – (18,84x133,333) = 2512 – 2512 = 0 W
Rotation de l’engrènement de (B) : (18,84x133,333) – (100x25,12) = 2512 – 2512 = 0 W

Si les deux couples rouge et noir avaient pour origine une charge.
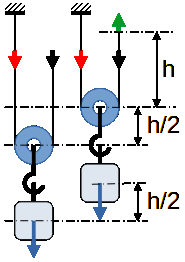
Les 25,12 rad/s du pignon planétaire mauve, correspondraient à une hauteur (h).
La charge serait donc levée d’une hauteur (h/2) correspondant à 12,56 rad/s.
Puissance constatée grâce à la gravité : 200x12,56 = 2512 W
Avec un point fixe (non libre) la force rouge reste fixe.
Par contre, avec le train d’engrenages asymétrique, la force rouge se déplacerait avec les d’engrènements du pignon satellite marron, en s’opposant à la force noire. Ce serait similaire au système à contrepoids sans la contrainte du contrepoids.
Rien ne se perd, rien ne se crée, tout se transforme.

[JLF]

Bonjour,
Je vous présente mes excuses pour les imperfections du texte et schéma à la fin du précédent message.
Voici la correction:
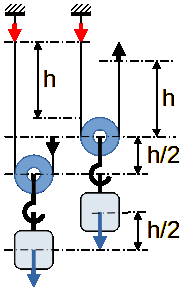
Si les deux couples rouge et noir avaient pour origine une charge.
Les 25,12 rad/s du pignon planétaire mauve, correspondraient à une hauteur (h).
La charge serait donc levée d’une hauteur (h/2) correspondant à 12,56 rad/s.
Puissance constatée grâce à la gravité : 200*12,56 = 2512 W
Avec un point fixe (non libre) les forces rouge et noire restent fixes.
Par contre, avec le train d’engrenages asymétrique, les forces rouge et noire, équilibrées, se déplaceraient avec les points d’engrènement du pignon satellite marron. Ce serait similaire aux systèmes à contrepoids ou la gravité déplace le point d’équilibre sur la périphérie de l’axe de la poulie pour garder sa verticalité. Rien ne se perd, rien ne se crée, tout se transforme.
Le pignon planétaire orange ne tournerait pas : il serait contraint mécaniquement par son couple qu’il transmettrait sur le pignon satellite marron, mais ne recevrait pas de couple du pignon planétaire mauve.
Pendant sa rotation, le pignon satellite marron, équilibrerait les couples égaux et opposés (rouge et noir), qu’il recevrait des pignons planétaires. Cependant il ne pourrait pas s’opposer au couple vert.