Un mélange suspect
-
Mmathtous dernière édition par
Etant donné un paquet de X cartes à jouer, X devant être supérieur à 1 mais
aussi grand qu'on veut ( on peut réunir plusieurs jeux ), on prend la première
carte du paquet ( celle du dessus ) et on la défausse ( on la jette ), puis on place
la suivante
sousle paquet.
On recommence : on jette la nouvelle carte du dessus et on place la suivante
sous le paquet. Et ainsi de suite jusqu'à ce qu'il ne reste plus qu'une seule carte
dans le paquet.
La question consiste à savoir quelle est cette dernière carte, autrement dit quelle
était sa position originelle dans le paquet.
Par exemple, s'il y avait 5 cartes au début, c'est celle qui occupait la position N° 2 qui reste en dernier.
-
Pour donner une piste, le cas où X est une puissance de 2 est assez intéressant...
-
Mmathtous dernière édition par
Oui, mais c'est le plus simple ...
-
c'est vrai, mais ça aide aussi pour les autres cas

-
Mmathtous dernière édition par
Naturellement, la formule traîne un peu partout sur internet.
Le but est de mettre en place une démonstration rigoureuse.
-
Ccarlun dernière édition par
Bonsoir,
Intéressant ce problème.
Une solution pratique se profile après simulation (sans l'aide d'internet) :Pour N cartes, c'est la carte en position P qui restera la dernière.

Mais je ne sais pas comment affiner l'algorithme
P=2N-(la 1° puissance de 2 ≥ N); je n'ai que +-*/ en poche et encore beaucoup à apprendre.Pour la démonstration?! Alors là...
 .
.(je cherche encore.)
A+-*/
-
Mmathtous dernière édition par
Oui, on peut ainsi "subodorer" la réponse.
Pour la démonstration, il doit en exister plusieurs. Celle que j'ai est assez délicate : il faut commencer par envisager des cas particuliers. On utilise des raisonnements par récurrence.
Je peux la tenir à disposition, mais comme pour les articles de mon site, elle est en .PDF : il faut Acrobat Reader pour la lire.
-
Ccarlun dernière édition par
Bonjour,
Curieux, je veux bien prendre connaissance de cette délicate démonstration...
J'ai chercher dans ma petite tête une manière de contourner "(la 1° puissance de 2 ≥ N)" en pensant au logarithme en base 2.
L'algorithme devient:
p=2n−2(ent(log(base2)n)+1)p=2n-2^{\left( ent\left(\log (base 2)n\right)+1\right)}p=2n−2(ent(log(base2)n)+1)(Je ne sais pas s'il existe une autre manière d'isoler la partie entière d'un résultat autrement que par Ent() )
A+-*/
-
Mmathtous dernière édition par
Ca ne marche pas.
Voici pourquoi :
appelons 2k2^k2k la plus grande puissance de 2 strictement inférieure à N, et 2k′2^{k'}2k′ la plus petite puissance de 2 supérieure ou égale à N.
On a évidemment k' = k+1.
Mais : 2k2^k2k < N ≤ 2k′2^{k'}2k′
Donc : k < log2log_2log2 N ≤ k'.
Les inégalités sont ... < ... ≤ ... , donc k' n'est pas la partie entière de log2log_2log2 N. Il faudrait pour cela que les inégalités soient ... ≤ ... < ...
Ca ne marche pas lorsque N est lui-même une puissance de 2 : vérifie sur un exemple.C'est bien compliqué d'utiliser des logarithmes : l'écriture en base deux est me semble-t-il plus simple, mais pose le même problème dans le cas où N est une puissance de 2.
Pour ce qui est de ma démonstration, je te l'envoie à l'adresse mail communiquée sur mon site. N'oublie pas qu'il faut Acrobat Reader ( ou équivalent ) pour lire les PDF.
-
Ccarlun dernière édition par
Salut,
Merci pour ta réponse.
Ben oui :frowning2: , j'aurais dû le voir tout seul:Pour N=12 => log 2_22 (12)≈3,... => 3+1=4
Pour N=15 => log 2_22 (15)≈3,... => 3+1=4
Pour N=16 => log 2_22 (16)=4 => 4+1=5 !!!! au lieu de 4 qu'il faudrait.Par ailleurs, peut-on trouver une manière d'isoler la partie entière d'un résultat autre que via Ent() ?
A+-*/
-
Mmathtous dernière édition par
La fonction "partie entière" est une vraie fonction mathématique.
On la note souvent E(x), ou encore [x], ou encore pareil mais sans fermer les crochets en haut ( pas clair ? ).
Ne pas confondre avec la fonction informatique Int(x) qui ne pose pas de problème lorsque x est positif, mais peut en poser ( selon les langages ) lorsque x est négatif.PS : as-tu reçu le mail avec la démonstration ?
-
Ccarlun dernière édition par
Bonsoir,
mathtous
Les inégalités sont ... < ... ≤ ... , donc k' n'est pas la partie entière de log2log_2log2 N. Il faudrait pour cela que les inégalités soient ... ≤ ... < ...
Ca ne marche pas lorsque N est lui-même une puissance de 2 : vérifie sur un exemple.Si
Pour N=15 => log 2 (15)≈3,...
Pour N=16 => log 2 (16)=4Qu'en est-il si je prends log2log_2log2(N-1)?
La formule devient alors:
p=2n−2(ent(log2(n−1))+1)p=2n-2^{\left( ent(log_{2}(n-1))+1\right)}p=2n−2(ent(log2(n−1))+1)
et le tour est joué non?
A+-*/
-
Mmathtous dernière édition par
Si.
Le but n'est point tant de trouver une "formule" que de la démontrer ...
-
Ccarlun dernière édition par
'soir,
Et pourtant, en ce qui me concerne, cette étape m'a beaucoup intéressée.

J'ai constaté que les étapes des puissances de 2 (2,4,8,16,32,...) étaient primordiales et base du calcul amenant au résultat P.
(d'où le recours à la fonction log2log_2log2() )$\ p=n-\left(2^{\left( ent(log_{2}(n-1))+1\right)}-n\right) \$
$\ p=n-2^{\left( ent(log_{2}(n-1))+1\right)}+n \$
$\ p=2n-2^{\left( ent(log_{2}(n-1))+1\right)} \$
Mais je ne sais pas comment entamer une démonstration. Je vais lire attentivement celle que tu m'as envoyée même si elle ne reprend pas explicitement l'algorithme ici présent.
Merci beaucoup encore
A+-*/
-
Mmathtous dernière édition par
C'est une question de point de vue.
Pour moi, la formule ( ou la "formulation" du résultat ) est secondaire.
Comme tu le fais remarquer, le cas particulier des puissances de 2 est primordial.
Tu verras que je l'ai étudié à part ( en premier lieu ) dans ma démonstration.PS : arrives-tu à charger les PDF sur mon site ?
Bonne lecture, A+
-
Ccarlun dernière édition par
mathtous
PS : arrives-tu à charger les PDF sur mon site ?r'soir,
Je viens encore de tenter un essai pour télécharger un problème depuis ton site mais ça ne fonctionne pas: tout se fige et j'ai beau attendre des plombes plus rien ne se passe.
Par contre le docu PDF envoyé sur mon mail, RAS.
A+-*/
-
Mmathtous dernière édition par
Bonjour,
Bizarre ... et dommage.
Il est vrai que le chargement peut être plus ou moins long, surtout lors du premier chargement : plusieurs secondes ( mais pas plusieurs heures ). Il arrive aussi que Firefox se bloque ( c'est assez fréquent ces temps derniers ).
Je viens de réessayer sous Firefox et sous IE : ça marche.
Sous Firefox, assure-toi que dans l'onglet Outils - Modules complémentaires - Plugins, il figure bien Adobe Acrobat. Ainsi que dans Outils - Options - Applications.
Sinon, essaie sous IE.
Tiens-moi au courant.
A+
MT
-
Ccarlun dernière édition par
'jour,
J'ai vérifié les points que tu as mentionnés.
(j'suis pas spécialiste...)Voici ce qui se fige:
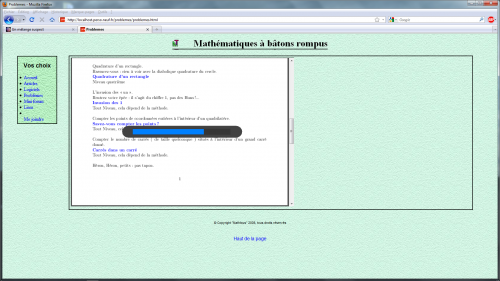
A+-*/
-
Mmathtous dernière édition par
Donc, tu parviens tout de même à charger un fichier PDF : celui contenant les liens vers les différents problèmes.
Puis le chargement se bloque.
Je vois également une autre anomalie : la page PDF ( ce qui est en blanc ) devrait occuper l'ensemble du frame ( dans le cadre, il ne devrait pas y avoir une zone verte vide ).
Moi non plus je ne suis pas spécialiste ... peut-être cela vient-il des options d'affichage ? A moins que ta version de Firefox ne soit ancienne ?
Que le chargement bloque la page doit cependant avoir une autre cause, mais j'ignore laquelle, d'autant plus que le fichier souhaité est tout petit ( ce qui n'est pas le cas de certains articles ).
Si en réessayant ( essaie aussi avec IE ) tu as toujours des difficultés, je te ferai parvenir l'énoncé ( Savez-vous compter les points ... ) par mail.
MT