asymptote !!! help

j'ai une question dans mon dm que je n'arrive pas a résoudre :
en déduire que C admet une asymptote DELTA en + infinie.
Précisez la position de C par rapport a DELTA.
f(x) = (x+1)exp(-1/x)

merci de votre aide

Bonjour,

f(x) = $x+1)^{(-1/x)}$

Pour étudier un comportement asymptotique, on a vu en 1re qu'il fallait étudier les limites de la fonction.

As-tu étudier les limites de f ?

D'après ton énoncé, il faudrait le faire en + infini...

J'espère que tu avais cherché l'exercice avant de poster ton message :razz:

oui oui j'ai cherché ! la limite en + inf' de f c'est + inf'

après les limites il faut trouver quoi ?

Tu es sûre de ça ?

lim (x+1) = + infini par somme
lim (-1/x) = $0^-$ par quotient

Et quand un nombre est affecté d'une puissance 0, on a... ?

(A vérifier tout de même, mais je pense que c'est ça.)

oui oui je suis sur je l'ai fais avec ma soeur. mais après je suis bloqué !

salut tous les deux

gare, il y a un petit piège. j'utilise la définition :

$(x+1)^{-1/x} = \text{e}^{\frac{-1}{x}\ln(x+1)$
or, lorsque x →+∞, on a ln(x+1) / x → 0 (limite ± connue)

donc f(x) → 1.

je suis perdue

Je ne comprend pas vraiment pourquoi on inclue un ln, Zauctore ?

En tous cas, marie, prennons un exemple,

$6^0$ = 1

La, tu es d'accord ? Un réel affecté d'une puissance 0 est égal à 1.

Ici, on voit que lim (-1/x) = 0 lorsque x tend vers +∞.
Donc la limite de n'importe quel réel affecté de la puissance (-1/x) sera $1^-$ lorsque x tend vers +∞.

Ici, lim (x+1) = +∞ lorsque x tend vers +∞.
Donc on a (
attention: mon écriture n'est pas valable dans un devoir, c'est juste pour illustrer) :

(+∞ $^0$ = 1

Si tu as un saisis ceci,
tu dois bien avoir lim $(x + 1)$ ^{(-1/x)} $1^-$ lorsque x tend vers +∞.

Je sais pas si tu m'as suivis.. Mais sinon, n'hésite pas à poser tes questions.

moi je l'ai fais avec ma soeur et on trouve + infini car :

lim de x+1 = + infini, lim de (-1/x) = 0 et ensuite on ajoute l'exponentielle, exp (-1/x) = 1 donc lim f(x)=+ infini car c'est 1 fois +infini si on remplace dans la formule par les limites...

la limite d'une fraction est toujours = 0 quand c en + infini ou en - infini

La limite d'une inverse est 0 lorsque X tend vers +∞ ou -∞. Mais pas forcément d'une fraction.

Exemple : lim (x/4) = +∞ lorsque x tend vers +∞

Mais ici, c'est bien une inverse, donc on a lim (-1/x) = $0^-$ lorsque x → +∞

Et pas besoin d'exponentiel à ce niveau, les propriétés de 1re fonctionnent.

lim $x^{(-1/x)}$ = $1^-$ lorsque x → +∞

Car pour tout x ∈ $mathbb{R}$ *, $x^0$ =1

oui pour ca je suis d'accord c'est ce que j'ai écris, exp(X) = 1

Attends... pour toi, exp = exposant, ou exp = exponentielle.

Parce que j'ai peur qu'il y ait eu confusion..

exponentielle

En relisant tous tes postes, je crois, qu'en effet, il y a eu confusion. Je pensais que exp = exposant pour toi. Donc.. Oublie tout ce que j'ai dit :rolling_eyes:
Enfin, pour ton exercice en tous cas..

oui donc voila je suis d'accord que exponentielle de (-1/x) = 1

mais je ne sais pas comment faire ensuite pour trouver l'asymptote

Etant donné que je ne suis pas sûr de maitriser le sujet.
Je préfère laisser Zauctore, ou un autre, t'expliquer tout cela.
Encore désolé d'avoir créer confusion.

ah ok il y avait que toi qui me repondai mais bon...

bon, marie reprenons :

ta fonction c'est

1° $\times e^{-1/x}$

ou bien

2° $f(x) = (x+1)^{-1/x}$

merci de préciser pour lever une ambiguïté stp

ma fonction c'est bien la deuxieme

euh nn nn la premiere pardon avec exponentielle

bon alors sa courbe est déjà :

<img src="http://www.mathforu.com/transfertfichier/fichiers/112-graphe-de-la-fonction-r-n.jpg" alt="graphe de la fonction
"title="graphe de la fonction
">
d'ailleurs tu as vu que la limite de f en +∞ est +∞ puisque l'exponentielle tend vers 1.

maintenant, on peut supposer que l'équation de l'asymptote est y = x+1, non vu le graphique.

évaluons f(x) - (x+1).

c'est (x+1) (e^(-1/x) - 1).

si la limite de e^(-1/x) - 1 est 0 lorsque x tend vers +∞, alors tu auras prouvé que la courbe de f admet l'asymptote y = x+1 au voisinage de +∞.

oui c ce que j'ai trouvé
et ta courbe tu l'as faites sur géogébra ?

et donc l'asymptote est oblique c'est bien ca ? pour la tracer je dois faire comment avec géogébra si tu sais t'en servir ? stp

sur geogebra (dsl j'étais parti dans l'a-m) voivi ce que je tape dans la zone de saisie : *(x+1)exp(-1/x)

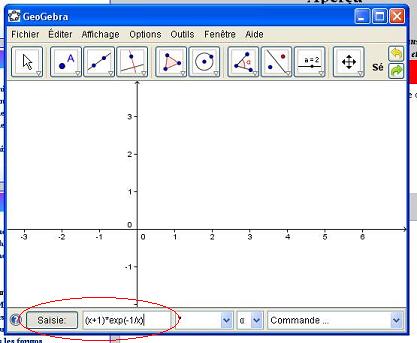
$fichier math$

ensuite tu presses entrée et tu obtiens :

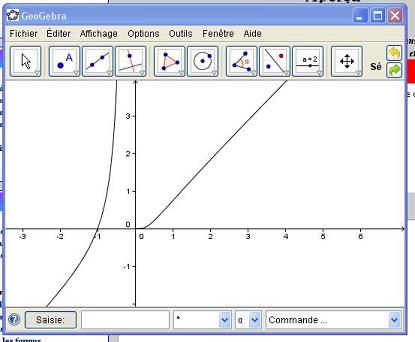
$fichier math$

il ne reste plus qu'à jouer sur les propriétés couleur - style (pour l'épaisseur) pour avoir un affichage plus joli.

voilà.

autre chose ?