intervalle et fonction
-
Hhelene34 dernière édition par
Bonjour, j'ai un dm comprenant fonction et intervalle.
- On me demande dans quel intervalle varie f(x) lorsque x varie dans [-1 ; 5]?
Cela veut dire quel est le minimum et le maximum ? - Comment doit on faire pour determiner pour quelles valeurs de x comprises entre - 1 et 5, le nombre f(x) est il positif si on a pas la fonction, j'ai que un dessin
- On me demande dans quel intervalle varie f(x) lorsque x varie dans [-1 ; 5]?
-
Bonsoir,
- A partir de la courbe, détermine pour x compris entre -1 et 5 sur quel intervalle est f(x).
- Tu prends les parties de la courbe ou f(x) est positif.
-
Hhelene34 dernière édition par
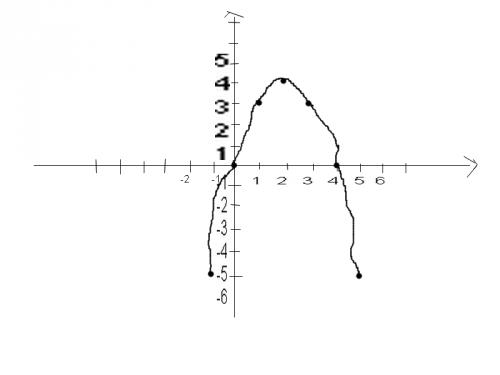
Voila la courbe a peu pres !
Son tableau de valeurs est :x -1 0 1 2 3 4 5
y=f(x) -5 0 3 4 3 0 -5
-
Hhelene34 dernière édition par
Donc pour la question 1:
S = [-5 ; 4 ] ?
Et pour la 2 :
S = ]0;4[ ??
-
Zauctore dernière édition par

salut
oui c'est simplement de la lecture graphique
-
ok
-
je dirai plutôt [1 ; 4] au sens large.
voilà !
-
-
Hhelene34 dernière édition par
Maintenant je dois dresser le tableau de signes de f sur [-1;5]
Mais comment faire si je n'ai pas le 'nom' de la fonction ?
-
Zauctore dernière édition par

Hélène, son nom c'est f ! ça donne négatif puis positif puis négatif selon les intervalles de gauche à droite.
il y a d'autres questions dans cet exo ?
-
Hhelene34 dernière édition par
Ah oui d'accord !
Apres il faut
1-resoudre graphiquement dans [-1;5] l'inequation f(x)<3
2-Completer le tableau de variations de f
3- Pour quelle valeur de x la fonction f admet elle un maximum sur [-1;5]
4- Construire C1 et C2 les representations respectives des fonctions g et h définies par g(x)=f(x+1) et h(x)=|f(x)|
-
Zauctore dernière édition par

Alors
1- résoudre graphiquement dans [-1;5] l'inéquation f(x)<3
pour cela il suffit de tracer la droite y = 3 et de regarder ce qui est "en-dessous" de celle-ci
2- Compléter le tableau de variations de f
rien à dire
3- Pour quelle valeur de x la fonction f admet elle un maximum sur [-1;5]
antécédent du max à lire sur l'axe des abscisses.
4- Construire C1 et C2 les représentations respectives des fonctions g et h définies par g(x)=f(x+1) et h(x)=|f(x)|
pour h, on rend tout positif : on renverse de l'autre côté de l'axe des x la "partie négative" de la courbe de f par symétrie axiale
pour g(x) = f(x+1) essie par exemple de te servir du tableau de nombres de f pour trouver g(0), g(1), ... etc.
-
Hhelene34 dernière édition par
Ok je vais essayer tout ca ! Et je vous dirai ce que je trouve!
-
Zauctore dernière édition par

ok
à plus tard !
-
Hhelene34 dernière édition par
-
Alors pour le tableau de signe on trouve :
x -1 0 4 5
f(x) - + - -
pour f(x)<3
S = [-1 ; 1[U]3;5] -
pour le maximum f en admet un egal a 4 pour x=2
-
et pour les droites : f(x+1), on retrouve la meme courbe, un cran plus haut, et pour la valeur absolue, je ne comprends pas comment faire!
-
-
Hhelene34 dernière édition par
Rectification :
Pour la droite f(x+1), elle se decale de un rang vers la droite
-
Attention, f(x+1) n'est pas représenté par une droite (et est encore moins une droite...). Es-tu sûre que la courbe est décalée vers la droite ?
Pour les valeurs absolues, lorsque les valeurs de f(x) sont positives tu ne changes rien et quand elles sont négatives tu les changes en -f(x) (qui est alors positif)...
-
Hhelene34 dernière édition par
Oui j'ai trouvé, la courbe monte bien d'un cran et ne se decale pas!
Et pour les valeurs absolues j'ai aussi trouver!
Merci !
-
Euh non elle ne monte pas non plus...
-
Hhelene34 dernière édition par
A bon ?!
-
oui... tu peux poser g(x)=f(x+1) si tu veux et essayer de tracer quelques points de cette nouvelle fonction sur le graphe !