Second problème de l'élastique
-
Aanthony59 7 oct. 2009, 14:17 dernière édition par
Bonjour à tous !
J'ai besoin d'un peu d'aide,
J'ai le problème suivant,
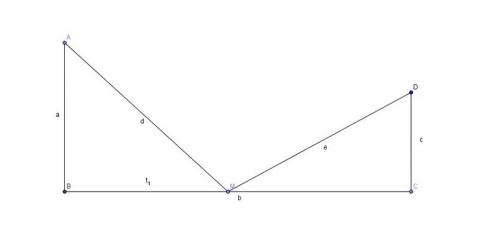
BC=7cm, AB = 3cm, et CD = 2cm
BM = x
On cherche pour quelle(s) positions(s)s du point M le triangle AMD est rectangle.
Les questions sont :- Trouver les réels et tels que, poujr tout réel x, x²-7x+6=(x+)²+
- Trouver ( grâce a une équation) la ou les valeurs de x telle(s) que AMD est rectangle en M. [ J'ai conjecturer que c'était x=1 et x=6 ]
-
Zorro 7 oct. 2009, 15:19 dernière édition par
Bonjour,
Ton énoncé est incomplet ....
Trouver les réels
(les quels ?)et tels que,poujr tout réel x, x²-7x+6=(x+)²+
expression incomplète !
-
Aanthony59 7 oct. 2009, 15:26 dernière édition par
Excuse moi ^^"
Trouver les réels α et β tels que ....
pour tout réel x, x²-7x+6=(x+α)²+βVraiment désolé.
-
Zorro 7 oct. 2009, 15:32 dernière édition par
La méthode d'identification pour une fonction polynôme est expliquée sur ce forum : http://www.math...ours-90.html
-
Aanthony59 7 oct. 2009, 15:35 dernière édition par
On peut utiliser cette explication malgré que je n'ai pas encore appris ?
-
Zorro 7 oct. 2009, 15:39 dernière édition par
Autre méthode : en développant (x+α)² + β
Et tu dois avoir l'égalité pour x = 0 , cela donne une première équation
Et tu dois avoir l'égalité pour x = 1 , cela donne une deuxième équation
Avec les 2 éqautions tu trouves α et β
-
Aanthony59 7 oct. 2009, 15:45 dernière édition par
Si je développe j'obtient x² + 2xα +α² +B =0 ?
-
Zorro 7 oct. 2009, 15:49 dernière édition par
Non tu as : pour tout réels x on doit avoir x² - 7x + 6 = x² + 2αx + α² + β
-
Aanthony59 7 oct. 2009, 15:51 dernière édition par
Je tombe sur : -2xa -B -a² -7x =-6
-
Zorro 7 oct. 2009, 15:54 dernière édition par
soit pour x = 0 quelle équation ?
Pour x = 1 quelle équation ?
Pour x = -1 quelle équation ?
-
Aanthony59 7 oct. 2009, 15:58 dernière édition par
Pourquoi dois-je remplacer x par 0/1/-1
-
Zorro 7 oct. 2009, 16:11 dernière édition par
C'est une méthode parmi d'autres ! VOir 17h39
Autre méthode , as tu vu la forme canonique ?
-
Aanthony59 7 oct. 2009, 16:13 dernière édition par
C'est quoi la forme canonique ?
-
Zorro 7 oct. 2009, 16:14 dernière édition par
Alors prends soit la méthode d'identification soit celle de 17h39
-
Aanthony59 7 oct. 2009, 17:03 dernière édition par
Peut tu m'expliquer la méthode de 17h39, je dois remplacer x par 0 .... ou tomber sur =0 ....
-
IIron 7 oct. 2009, 18:49 dernière édition par
Bonsoir,
Je n'ai pas fait l'exo mais ...
L'égalité comporte 3 inconnues x, α et β.
Elle doit être vérifiée pour tout x. On peut donc choisir les valeurs de x que l'on veut, l'égalité doit rester vraie.La "méthode de 17h39" consiste à prendre 2 valeurs pour x de notre choix. Cela nous conduit à un système de 2 équations à 2 inconnues que l'on sait résoudre.