fonction volume d'un placard

Bonsoir, je dois faire cet exercice que je ne n'arrive pas, j'aurai donc besoin d'aide :s

Enoncé;
On veut réaliser dans l'angle d'un plan de travail, un placard ayant la forme d'un parallélépipède rectangle.
Pour des raisons pratiques, si sa largeur est x, sa profondeur est 12-x et la hauteur est égale à la profondeur. (Les dimensions sont exprimées en dm)

1/ Vérifier que le volume V(x) en dm3 de ce placard est: V(x) = x³-24x²+144x

2.a/ Etudier les variations de la fonction f definie sur [0;12] par f(x) = x³-24x²+144x
b/ Tracer la courbe C représentative de la fonction f dans le repère orthogonal (unités: 1 cm pour 1 dm en abscisses et 1 cm pour 25 dm³ en ordonnées). On précisera la tangente à C au point de l'abscisse 8.

3/ Utiliser l'étude précidente pour le travail suivant.
a/ Déterminer la largeur l du placard pour laquelle son volume est maximal. Quel est ce volume?
b/ Indiquer pour quelle(s) valeur(s) de la largeur le placard aura un volume égal à 175dm³. ( on donnera les résultats à 10-1 près)

Merci d'avance ^^

quel est le problème?
volume = l x L x P

bonjour
pour résoudre cet exercice, il faut avoir des notions de dérivée, discriminant pour les questions 2a) 2b) et 3a)

je me demande si en 1S vous avez déjà abordé ces notions

pour la 3b) puisqu'on parle de $10^{-1}$ près alors il faut comprendre que la réponse est "approximative" donc on peut utiliser sa calculatrice (tableau de valeurs) pour résoudre une certaine équation.

euh je sais pas ce que c'est les discrimants j'aurai bien besoin d'aide à partir du 3 =/

Semper-Eadem
euh je sais pas ce que c'est les discrimants j'aurai bien besoin d'aide à partir du 3 =/
Bonjour Semper-Eadem,

Si tu as besoin d'aide uniquement à partir du 3), j'en déduis que tu as su calculer f'(x) et donc que tu as vu la dérivation.

f'(x) est un polynome du second degré. Je suppose encore que si tu as su étudier son signe, impératif pour en déduire les variations de f question 2), c'est que tu as vu également les polynomes du second degré (donc les discriminants).

Si tu as vu ces deux chapitres là, c'est que vous êtes bien avancés dans le programme. Sinon, je ne pense pas que cet exo soit réalisable.

Pour la 3), il faut utiliser le tableau de variation de la fonction f question 2a).
La courbe Cf admet un maximum local pour x = 4 dm, valeur pour laquelle la dérivée s'annule.

Le volume maximum est alors Vmax = f(4). A toi de calculer, sans oublier l'unité !

Pour la 3b), voir la réponse de netprof92 (calcullette). Toutefois, recherche d'abord une approximation avec la courbe Cf et vérifie s'il existe une ou plusieurs possibilités pour obtenir ce volume ?

La dérivée n'est pas au programme de première

Et bien j'ai du me tromper sur toute la ligne puisque j'ai pas trouvé dans le tableau de variation puisque j'ai pas trouvé ; Cf admet un maximum local pour x = 4 dm

stephaneenligne
La dérivée n'est pas au programme de première

Bonjour Stéphane,

Il me semble qu'en 1ère S, la dérivation est bien au programme : approximations affines, dérivabilité en un point, équation de tangente, dérivées, sauf la dérivée de fonctions composées qui n'est vue qu'en Term).

En section ES, effectivement, les dérivées sont vues en début Term ... sauf erreur de ma part bien entendu.

Crdlt

Semper-Eadem
Et bien j'ai du me tromper sur toute la ligne puisque j'ai pas trouvé dans le tableau de variation puisque j'ai pas trouvé ; Cf admet un maximum local pour x = 4 dm

Que trouves-tu ?

As-tu tracé la courbe Cf avec la calculette ?

Ton tableau de variation est-il en adéquation avec ta calculette ?

Bah je l'ai tracé à la calculatrice mais je crois que c'est trop grand pour s'affichent et j'arrive pas à réduire le graph ...

essaie ces réglages :

X mini = 0
X maxi= 12

Y mini = 0
Y maxi = 270

Iron
stephaneenligne
La dérivée n'est pas au programme de première

Bonjour Stéphane,

Il me semble qu'en 1ère S, la dérivation est bien au programme : approximations affines, dérivabilité en un point, équation de tangente, dérivées, sauf la dérivée de fonctions composées qui n'est vue qu'en Term).

En section ES, effectivement, les dérivées sont vues en début Term ... sauf erreur de ma part bien entendu.

Crdlt

exact exact ! je demande pardon!

Ma "calculatrice" donne ceci

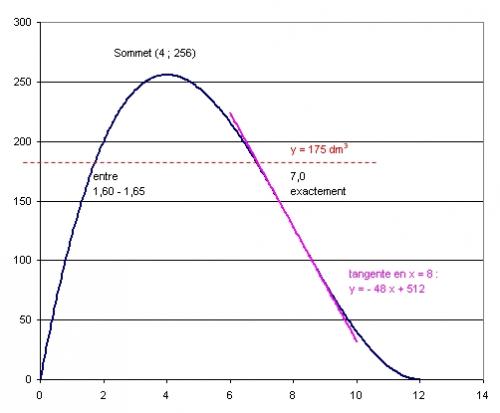
$fichier math$

Il n’y a aucun souci, Stéphane