Traduire l'aire hachurée par une fonction de x et étudier son domaine de définition et ses extremums
-
Aanthony59 dernière édition par Hind
Bonjour pouvez vous m'aider à avancer dans mon exercice merci

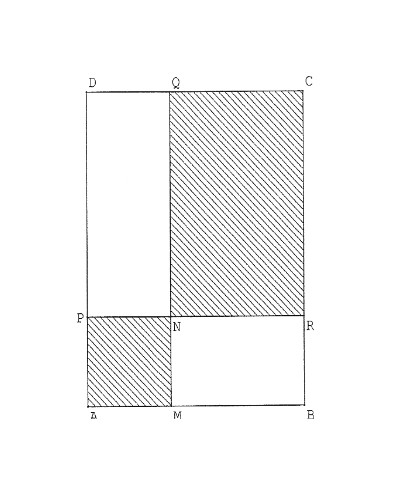
Le rectangle ABCD a pour dimension AB=3 et AD=4.
Le point M se déplace sur le segment [AB].
On note x la distance AM.Pour chaque point M on construit le carré MNPA et le rectangle NQCR.
a) Exprimer en fonction de x l'aire hachurée que l'on notera f(x).
b)Pour quelles valeurs de x,f est-elle ici définie ?
c) Pour quelle valeur de x cette aire est-elle minimale ?
d) Donner alors cette valeur minimale.Figure
a) L'aire hachurée: X²+(4-x)*(3-X)
b) x définie [0;4]J'arrive pas à faire le petit c et d merci beaucoup
-
Aanthony59 dernière édition par
L'air est minimum pour x=0
J'dois résoudre X²+(4-x)*(3-x)=0
C'est bien cela
-
Mmathtous dernière édition par
Bonjour,
Pour la question a) , c'est juste : mais développe et réduis
Pour la b) c'est faux :
x doit être inférieur à 3 puisque M est situé sur le segment [AB]
De plus, j'excluerais les valeurs extrêmes 0 et 3 pour lesquelles le carré ou le rectangle sont "aplatis". Mais on peut néanmoins les accepter.
Pour la question c), étudie les variations de f. Calcule f '(x).
-
Sstudypass dernière édition par
bonjour,
Tu ne dois pas supposer que l'aire est minimum en zero. Tu dois etudier la fonction et recherche un minimum pour celle ci.
Tu sais comment faire ?
-
Sstudypass dernière édition par
désolé Mathtous je n'avais pas vu que tu avais repondu. :razz:
-
Mmathtous dernière édition par
Pas grave.
J'ai fait remonter un de mes vieux sujets : si le coeur t'en dit ...
-
Sstudypass dernière édition par
J ai vu .. les petits triangles héroniens... ca me trotte sur un bout de feuille.. j y'reflechis
 mais ca fait longtemps pour moi les maths de ce niveau.
mais ca fait longtemps pour moi les maths de ce niveau.
-
Mmathtous dernière édition par
C'est déjà ça : quelqu'un qui accepte de me dépanner : merci.