Exercice sur les fonctions dans un repère.

Bonsoir à tous.

Voici un petit exercice qui me pose quelques soucis. Ce n'est pas très urgent j'ai le temps pour le faire.J'ai déjà beaucoup réfléchis dessus mais je coince et sa me perturbe.J'ai fais un schéma sur pain mais je ne sais pas comment le mettre sur le forum.
Si vous me dites comment mettre une image de pain sur le forum je la mettrai volontiers surtout que comme ca elle n'aura pas servit à rien.
Excusez moi pour les fautes d'orthographes s'il y en a (normalement j'ai tous corrigé )

f est la fonction affine définie par f(x)=2x-3.
Dans un repère orthonormé, d est la droite qui représente la fonction f
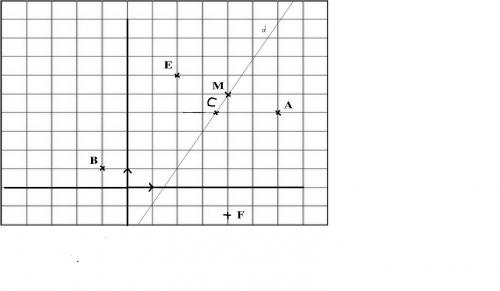
On donne les points : A(6;4) ; B(-1;1) ,C(7/2 ;4) ; E(2;6) , F(4;-3/2)

a) Construire la droite d et placer les points précédents.

b) calculer f(7/2). Le point C appartient-il à la droite d ? Justifier.

c) Soit M le milieu du segment [EA]. Calculer les coordonnées du point M. Le point M appartient-il à la droite d ? Justifier.

d) Montrer que le triangle AMC est rectangle en M

e) Que représente la droite d pour le segment [EA]? Justifier.

f) La droite d est-elle la médiatrice du segment [BF] ? Justifier.

b)f(7/2) = 2 × (7/2) - 3
=(14/2) - 3
=7-3
=4

Oui, le point C appartient à la droite d car lorsqu'on remplace x par 7/2 qui est l'abscisse du point C dans la fonction f on obtient l'ordonnée du point C. Donc on peut en conclure que C appartient bien à la droite d.

c) Pour calculer le milieu d'un segment j'utilise cette formule : (xa +xb)/2
= 8/2
= 4

(ya +yb)2
=10/2
=5

Donc le point M a pour coordonnées x=5 et y=4

Je fais comme précédemment sauf avec le point M cette fois ci f(5)
Au final on remarque que le point M appartient à la droit d car f(5)est égal à 4 (qui est l'ordonnée de M)

d)J'ai calculer AM=√5 MC=√1.25 et CA=√6.25
J'utilise la réciproque du théorème de pythagore et j'en conclus que AM²+MC²=CA² donc la triangle AMC est rectangle en M

e) Une médiatrice coupe un segment en son milieu et perpendiculairement ce qui est le cas de la droite d qui coupe le segment [EA] en son milieu perpendiculairement donc la droite d est la médiatrice du segment [EA].

f) J'ai utilisé la propriété ci : " Si un point est équidistant des extrémités d'un segment alors ce point appartient à la médiatrice de ce segment" Donc le point qui est le milieu de BF que j'ai nommé K est à égal distance de E que de A. Et on peut dire qu'il appartient à la droite d. Pour le reste de la démonstration je suis bloqué...

$fichier math$

Je vous dis merci d'avance et bonne soirée !

salut

pour l'image tu peux faire comme l'indique le chef Thierry dans ce message

@+

Alors la tu vois je te dois une fière chandelle Zauctore
Merci pour le conseil à présent j'ai pût mettre l'image que j'ai faites. Encore merci.

Bonsoir nawaka,

Je n'aurai pas le temps ce soir de t'aider, quelqu'un d'autre en aura la possibilité j'espère.

J'interviens juste pour te signaler que le point C se situe sur la droite d je pense (abscisse 7/2 = 3,5) ... un si beau dessin paint

Bonsoir,

J'ai édité , j'ai trouvé quelques réponses et j'ai changé le dessin de Paint. Merci de m'avoir faire remarquer l'erreur en passant Iron.
De toute façon si tu ne peux pas t'en occuper ce soir c'est pas grave j'ai le temps :).

Bonne soirée à vous tous.

Bonjour patient(e) nawaka,

Citation
a) Construire la droite d et placer les points précédents.
Ok, ta construction me semble correcte maintenant.

Citation
b) calculer f(7/2). Le point C appartient-il à la droite d ? Justifier.
Correct. f(7/2) = 4. Donc C(7/2;4) ∈ d

Citation
c) Soit M le milieu du segment [EA]. Calculer les coordonnées du point M. Le point M appartient-il à la droite d ? Justifier.
Correct aussi. M(4;5) et f(4) = 5 ⇒ M(4;f(4)) ∈ d

Citation
d) Montrer que le triangle AMC est rectangle en M
Ta réponse est correcte et bien justifiée.
Je te proposerais simplement de rester en fractions.
Une astuce pratique aussi lorsque tu utilises la réciproque de Pythagore, c'est de calculer les carrés des longueurs : ça évite souvent les "√".

Ici par exemple, tu calcules AM², CM² puis AC² en laissant sous forme de fraction :

AM² = (4 - 6)² + (5-4)² = 4 + 1 = 5
CM² = (4 - 7/2)² + (5-4)² = (1/2)² +1 = 5/4
AC² = (7/2 - 6)² + (4-4)² = (-5/2)² + 0 = 25/4

AM² + CM² = 5 + 5/4 = 20/4 + 5/4 = 25/4

Soit : AM² + CM² = AC²

D'après la réciproque du théorème de Pythagore, le triangle AMC est rectangle en M.

Citation
e) Que représente la droite d pour le segment [EA]? Justifier.
C'est toujours correct.
Les droites d et (EA) sont perpendiculaires d'après d)
M est le milieu de [EA]
La droite d coupe donc le segment [EA] perpendiculairement en son milieu M. d est donc la médiatrice du segment [EA].

Citation
f) La droite d est-elle la médiatrice du segment [BF] ? Justifier.
Finalement, c'est la seule question qui te pose prbl.

Citation
J'ai utilisé la propriété ci : " Si un point est équidistant des extrémités d'un segment alors ce point appartient à la médiatrice de ce segment"

Cette propriété ne va pas nous servir ici.

Citation
Donc le point qui est le milieu de BF que j'ai nommé K est à égal distance de E que de A. Et on peut dire qu'il appartient à la droite d. Pour le reste de la démonstration je suis bloqué...
La méthode est la bonne, je vais juste essayer de l'éclaircir un peu.

d sera médiatrice de [BF] si et seulement si :

| d coupe le segment [BF] en son milieu
| et
| les droites d et (BF) sont perpendiculaires.

Si une seule des ces 2 conditions n'est pas respectée alors d n'est pas médiatrice.

Je te propose de déterminer en premier lieu les coordonnées du point K milieu de [BF] et de vérifier ensuite si ce milieu appartient à la droite d.

Soit K le milieu du segment [BF] . . .
K ( $x_K$ ; $y_K$ ) (coordonnées à calculer)

Puis de vérifier si K appartient à la droite d en calculant $f(x_K$ ) comme tu l'as fait pour les points M et C dans les questions précédentes.

Voilà, à toi ...