Faire des calculs en utilisant les vecteurs
-
Aallanpompier dernière édition par Hind
Bonjour a tout les membres du forum mathématique !
Donc voilà, depuis lundi j'ai un DM de maths assez compliqué pour moi... Pour tout vous dire, j'ai etait absent 1 mois car j'ai eu de gros soucis de famille... Le prof ma demandé de faire se DM pour avoir quand meme un note avant la fin des notes ( Qui est pour Samedi... Dm a rendre pour demain. )Voilà l'énoncé avec se que j'ai fais pour le moment :
EX1 : Dans un repére orthonormé, placer les points :
A(3;1) B(2;3) C(-4;0) D(-3;-2)
a. Prouver que ABCD est un parallélogramme.
a. Xo=Xc+Xa/2=-4+3/2= -0.5
Yo=Yc+Ya/2=0+1/2= 0.5Xr=Xd+Xb/2=-3+2/2= -0.5
Yr=Yd+Yb/2=-2+3/2= 0.5On constate que O et R ont les mêmes coordonnées, donc O et R sont confondus. Dans le quadrilatére ABCD a ses diagonales [CA] et [DB] qui se coupent en leur milieu. Donc ABCD est un parallélogramme.
b. Calculer les diagonales, qu'en déduisez-vous ?
AC= √(xc-xA)²+(yC-yA)² = √50
BD= √(xD-xB)²+(yD-yB)² = √50
comme AC = BD : un parallélogramme qui a ses diagonales égales est un réctangle.
Là commence a être les difficultés => EX2 : Dans un repére orthonormé, placer les points
A(-2;6) B(2;-1) C(-3;3)
a. Determiner les coordonnées du point N tel que vecteur de BN=vecteur BA+BC
b. Determiner les coordonnées du point M tel que vecteur de OM=vecteur
AB+ACc. Quelle conjécture peut-on faire sur les points M,A et N ? La démontrer.
Algorithmique et fonction :
Soit F la fonction définie sur R par : f(x)=(x-3)²-4
- Calculer l'image de 7, puis f(-2).
Pour f(7) = (7-3)²-4 = 12
Pour f(-2) = (-2-3)²-4 = 21-
Tracer la courbe de la fonction f sur votre calculatrice et compléter son tableau de variations. ( Pas de calculatrice Graphique... :s Pas les moyens d'en acheter une... )
-
A l'aide de la courbe, donner une valeur approchée des antécédents de : 1; -4 et -5
-
Sans les calculers comparer f(-3,1) et f(2,2) puis f(racine de 10 ) et f(racine de 11 ). ( Justifier vos réponses )
Mille merci a vous !!!
Allan
-
IIron dernière édition par
Bonjour,
Normalement, on se limite à un seul exercice par post ! C'est plus clair et plus pratique.
EX1 :
a) N’oublie pas de présenter tes points :
Soit O et R les milieux respectifs des segments [AC] et [BD].b) Je préfère "diagonales de même longueur" à "diagonales égales" . . . mais tout ça me semble correct.
-
IIron dernière édition par
EX 2 :
De façon générale, les coordonnées d’un vecteur AB→AB^\rightarrowAB→ sont (x(x(x_B−xA-x_A−xA ; yyy_B−yA-y_A−yA)
Si w→w^\rightarroww→ = u→u^\rightarrowu→ + v→v^\rightarrowv→ alors
| xwx_wxw = xux_uxu + xvx_vxv
| et
| ywy_wyw = yuy_uyu + yvy_vyva) BN→BN^\rightarrowBN→ = BA→BA^\rightarrowBA→ + BC→BC^\rightarrowBC→
Tu peux donc partir du système :
| xNx_NxN – xBx_BxB = (xA(x_A(xA – xBx_BxB) + (xC(x_C(xC – xBx_BxB)
| et
| xNx_NxN – xBx_BxB = (xA(x_A(xA – xBx_BxB) + (xC(x_C(xC – xBx_BxB)b) Même méthode
-
IIron dernière édition par
EX 3 :
-
Correct
-
Si tu disposes d'un tableur et si tu sais un peu l'utiliser, tu peux tracer la courbe représentative.
Voici ce que cela donne (c'est une parabole) :
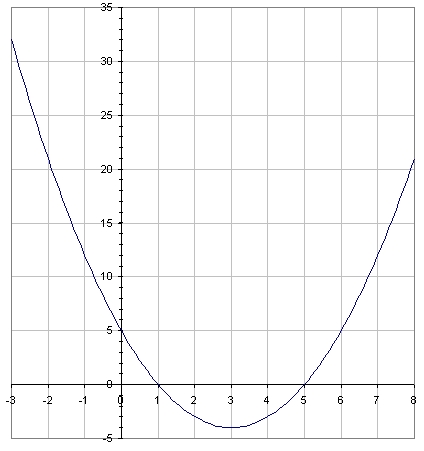
Le sommet a pour coordonnées (3;-4)
Ca devrait te permettre de poursuivre ton DM ...
-
-
Aallanpompier dernière édition par
Pour l'exercice 2 je fais comme tu demande puis je reste bloquer a un endroit...
Voilà ou j'en suis :
Xn-2 = (-2-2) + (-3-2)
Xn-2 = (-4) + (-5)
Xn-2 = -9Ensuite ?
Merci
Allan
-
Aallanpompier dernière édition par
EX 3 :
Mon tableau de variation ce fait ainsi :
X -∞ 3 +∞
f(X) → ( Qui déscend ) → ( Qui monte )
Entre les deux fléches je met 4 ?


- A l'aide de la courbe, donner une valeur approchée des antécédents de : 1 ; -4 et -5
Je trouve :
-antécédent de 1 ≈ 0.8
-antécédent de -4 ≈ 2.9
-antécédent de -5 = 3- Pas encore compris

Allan
-
IIron dernière édition par
allanpompier
Xn-2 = (-2-2) + (-3-2)
Xn-2 = (-4) + (-5)
Xn-2 = -9Ensuite ?
EXO 2 :
Tu isoles xNx_NxN = -9 + 2 = -7 et tu connais maintenant l'abscisse du point N : xNx_NxN = -7
Tu fais la même chose pour son ordonnée yN
Tu pourras tracer le point N (xN(x_N(xN ; yNy_NyN)
b) Même méthode pour déterminer les coordonnées de M
PS : Tu peux vérifier ton énoncé question c), c'est bien les points A, N et M ?
-
IIron dernière édition par
Citation
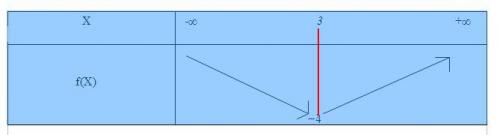
Entre les deux fléches je met 4 ?Non (pas "4", mais "-4"), pour x=3, il y a une simple barre (la valeur 3 fait partie de l'ensemble de définition de f). Sur cette barre tu inscris
-4 car c'est l'image de 3 par f.Edit : Ca c'est pour l'EXO 3 ... tu comprends la nécessité de créer un post par exo !
-
Aallanpompier dernière édition par
En effet, pour la question c. se sont les points M, A et N.
Ok j'ai compris a présent mais pour Yn je suis re-perdu... Je doit mettre quoi a la suite ?
Yn = ( ) + ( ).... ?
Allan
-
IIron dernière édition par
Citation
Je trouve :-antécédent de 1 ≈ 0.8
-antécédent de -4 ≈ 2.9
-antécédent de -5 = 3EXO 3 :
Commençons par l'antécédent de -4
Ton tableau de variation te donne la réponse exacte : f(3) = -4
donc l'antécédent de -4 est ... ?- L'antécédent de -5
Je sais que tu n'as pas de calculette, je t'ai donc précisé : "Le sommet a pour coordonnées (3;-4)"
Ce point correspond en fait à un minimum, bien illustré par la représentation graphique.
Si tu traces une droite horizontale en pointillés en partant de y = -5, est-ce que tu obtiens un/des points d'intersection avec la courbe Cf ?
quels sont alors les antécédents de -5 ?
- L'antécédent de 1.
Ta réponse n'est pas fausse. Mais si tu traces une droite horizontale en pointillés en partant de y = 1, combien de fois cette droite va-t-elle couper la courbe Cf ?
Combien la valeur -5 aura-t-elle d'antécédents ?
- L'antécédent de -5
-
IIron dernière édition par
allanpompier
... mais pour Yn je suis re-perdu... Je doit mettre quoi a la suite ?Yn = ( ) + ( ).... ?
EXO 2 question a)
Je me suis trompé à 13:09, je voulais noter :
Puisque BN→BN^\rightarrowBN→ = BA→BA^\rightarrowBA→ + BC→BC^\rightarrowBC→
| xNx_NxN – xBx_BxB = (xA(x_A(xA – xBx_BxB) + (xC(x_C(xC – xBx_BxB)
| et
| yNy_NyN – yBy_ByB = (yA(y_A(yA – yBy_ByB) + (yC(y_C(yC – yBy_ByB)... 2ème équation avec des y et non plus des x ! J'ai fait un copier-coller sans modifier, désolé.
-
Aallanpompier dernière édition par
Exo 3 :
Antécédent de -4 = 3
Antécédent de -5 = 0 ( car la courbe ne passe par ma ligne horizontale )
Antécédent de 1 = 2 ( car sur ma ligne horyzontale, 2 fois ma courbe y passe )Exo 2 :
Yn -(-1) = (6-(-1)) + (3-(-1))
Yn -(-1) = 7 + 4
Yn = 11 - 1
Yn = 10Ccl : N a pour coordonnées ( -7; 10 )
pour Xm et Ym peut tu me donner comme tu a fait pour N ?
Mille merci !!!
Allan
-
IIron dernière édition par
Citation
Exo 3 :Antécédent de -4 = 3
OuiCitation
Antécédent de -5 = 0 ( car la courbe ne passe par ma ligne horizontale )
Non. Effectivement, "la courbe ne passe par ma ligne horizontale"
donc -5 n'admet aucun antécédent par f tout simplement. Cela signifie qu'aucune valeur de x n'aura pour image -5.On ne te demande pas le nombre d'antécédents, mais le/les antécédent(s) éventuels. Là, il n'y en a aucun.
Citation
Antécédent de 1 = 2 ( car sur ma ligne horyzontale, 2 fois ma courbe y passe )
Encore une fois, on ne te demande pas le nombre d'antécédents ...
"1" admet effectivement 2 antécédents, mais on te demande lesquels ?
-
IIron dernière édition par
OM→OM^\rightarrowOM→ = AB→AB^\rightarrowAB→ + AC→AC^\rightarrowAC→
donc
| xMx_MxM – xOx_OxO = (xB(x_B(xB – xAx_AxA) + (xC(x_C(xC – xAx_AxA)
| et
| yMy_MyM – yOy_OyO = (yB(y_B(yB – yAy_AyA) + (yC(y_C(yC – yAy_AyA)Quelles sont les coordonnées du point O origine du repère ?
-
Aallanpompier dernière édition par
Antécédent de 1 = 0 et 6 ?
Voici mon tableau pour l'EXO 3 mais j'ai pas l'impression que sa soit sa !
Allan
-
Aallanpompier dernière édition par
Xm - Xo = (2-3) + (-4-3)
Xm - Xo = -1 + (-7 )
Xm - Xo = -8Yn - Yo = (-1-6) + (3-6)
Yn - Yo = -7 + (-3)
Yn - Yo = -10Les coordonnées du Point O est ( -8; -10 ) exact ?
Allan
-
IIron dernière édition par
Citation
Antécédent de 1 = 0 et 6 ?Non, mais je comprends ton erreur, elle est due à mon échelle des ordonnées.
Regarde mieux, les antécédents de 1 sont
environ0,8 et 5,2
-
IIron dernière édition par
allanpompier
Voici mon tableau pour l'EXO 3 mais j'ai pas l'impression que sa soit sa !Ca me paraît correct, il reste à ajouter une barre verticale traversante à x=3
-
Aallanpompier dernière édition par
Pour le tableau de variation : Je ne vois pas ou je pourrai mettre la barre Iron... :s
Pour la question c. pourrais-je avoir un coup de main ?
Allan
-
IIron dernière édition par
allanpompier
Les coordonnées du Point O est ( -8; -10 ) exact ?Non. Les coordonnées du Point O sont ( 0; 0 ) puisque c'est l'origine du repère !
-
IIron dernière édition par
Ici :
-
Aallanpompier dernière édition par
Donc je refais avec M :
Xm - 0 = (2-3) + (-4-3)
Xm - 0 = -1 + (-7 )
Xm = -8 + 0
Xm = -8Yn - 0 = (-1-6) + (3-6)
Yn - 0 = -7 + (-3)
Yn = -10 + 0
Yn = -10Les coordonnées du Point M est ( -8; -10 ) ?
-
IIron dernière édition par
yM = -10, j'ai ça aussi.
Par contre :
Citation
Xm - Xo = (2-3) + (-4-3)
Xm - Xo = -1 + (-7 )
Xm - Xo = -8Je ne trouve pas cette valeur pour xMx_MxM !
Avec : A(-2;6) B(2;-1) C(-3;3) et O(0;0)
Reprends cela de ton coté :
| xMx_MxM – xOx_OxO = (xB(x_B(xB – xAx_AxA) + (xC(x_C(xC – xAx_AxA)
-
Aallanpompier dernière édition par
Xm - 0 = (2-(-2)) + (-3-(-2))
Xm - 0 = 4 + (-1)
Xm - 0 = 3
Xm = 3 + 0
Xm = 3Corrécte ?
Allan
-
IIron dernière édition par
J'ai trouvé la même chose M (3;-10)
Citation
c. Quelle conjécture peut-on faire sur les points M,A et N ? La démontrer.
Cette dernière question sentait l’alignement des points à plein nez, mais apparemment, ce n’est pas le cas.Alors je n'ai pas d'idée, je ne vois à priori rein de particulier entre ces 3 points, si quelqu'un d'autre peut t'aider ...
Je dois quitter ... désolé
-
Aallanpompier dernière édition par
ok merci quand meme Iron pour ton aide !!!
Nous avions oublié une question...Ex3 4.4) Sans les calculers comparer f(-3,1) et f(2,2) puis f(racine de 10 ) et f(racine de 11 ). ( Justifier vos réponses )
Merci par avance
Allan
-
IIron dernière édition par
Pour cette dernière question, il faut utiliser le tableau de variation de la fonction f :
Elle est strictement décroissante sur l’intervalle ]-∞ ; 3 [
-3,1 et 2,2 appartiennent à cet intervalle.
Or -3,1 < 2,2 donc
f(-3,1) . . . f(2,2)
Rappel : une fonction croissante conserve l'ordre, une fonction décroissante inverse l'ordre.
Même principe pour les deux autres valeurs : √10 et √11 appartiennent à ]3 ; +∞[
f est strictement ... sur cet intervalle.
Or √10 < √11
donc f(√10) ... f(√11)
Bon courage pour la suite.
-
Aallanpompier dernière édition par
Pour cette dernière question, il faut utiliser le tableau de variation de la fonction f :
Elle est strictement décroissante sur l’intervalle ]-∞ ; 3 [
-3,1 et 2,2 appartiennent à cet intervalle.
Or -3,1 < 2,2 donc
f(-3,1) < f(2,2)
Rappel : une fonction croissante conserve l'ordre, une fonction décroissante inverse l'ordre.
Même principe pour les deux autres valeurs : √10 et √11 appartiennent à ]3 ; +∞[
f est strictement croissante sur cet intervalle.
Or √10 < √11
donc f(√10) < f(√11)
Corrécte ?
Allan
-
IIron dernière édition par
Non pour la 1ère
-3,1 < 2,2 donc
f(-3,1) > f(2,2) car f est strictement décroissante sur l’intervalle ]-∞ ; 3 [, elle inverse l'ordre !
Oui pour la 2ème.
√10 < √11
donc f(√10) < f(√11) car f est strictement croissante sur l’intervalle ]3;+∞[, elle conserve l'ordre
-
Aallanpompier dernière édition par
Merci Iron ! Comment justifier ? Peut tu le faire pour le premier ? J'essayerai de le faire pour le deuxiéme !
Allan
-
IIron dernière édition par
C'est déjà fait. J'ai mis en gras les justifications
car f est ...
Je quitte, à+
-
Aallanpompier dernière édition par
Un énorme merci Iron ! Au plaisir de te re voir sur un autre Poste !
Allan
