Résoudre cos (x) = E(x)
-
Ssneiv dernière édition par
Bonjour
je dois résoudre cette équation cos x = E(x) avec E la partie entière sur [0 ; pi/2].
qui peut m'aider SVP ?
-
Zorro dernière édition par

Bonjour,
Si x ∈ [0 ; 1[ que vaut E(x) ?
Si x ∈ [1 ; pipipi/2] que vaut E(x) ?
-
Ssneiv dernière édition par
sur [0 ; 1[, E(x) = 0
et sur [1 ; pi/2[ = 1
-
Ssneiv dernière édition par
donc il faut juste résoudre en deux parties alors ?
sur [0 ; 1[ cos x = 0
pui sur [1 ; pi/2] cos x = 1
-
Zorro dernière édition par

sur [0 ; 1[ , existe-t-il un x tel que cos(x) = 0 ?
sur [1 ; pipipi/2] , existe-t-il un x tel que cos(x) = 1 ?
-
Ssneiv dernière édition par
pour moi, cos x = 0 n'a pas de sol sur [0 ; 1[ car 0 = cos pi/2
et cos x = 1 non plus car 1 = cos 0
-
Ssneiv dernière édition par
mais l'énoncé dit qu'il faut démontrer que l'équation n'admet qu'une unique sol sur [0 ; pi/2]
-
Zorro dernière édition par

Moi je trouve aucune solution ...
En rouge partie entiere , en noir la fonction cosinus
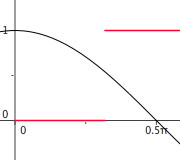
-
Ssneiv dernière édition par
qu'est ce que je fais ?
dois je aller voir mon prof ?
-
Zorro dernière édition par

Moi j'irais le voir ,
par contre sin(x) = E(x) admet 2 sol sur [0 ; pipipi/2] : 0 et pipipi/2
-
Ssneiv dernière édition par
ok merci bcp
-
Zorro dernière édition par

Je t'en prie !