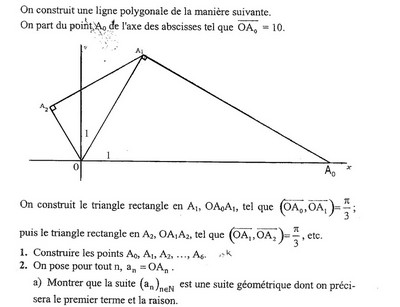
Devoir Maison sur les Suites

Bonjour tout le monde, j'ai actuellement un devoir de maths sur les suites. Après avoir galéré quelque temps je poste la 2ieme question du début de mon DM qui me pose problème car j'arrive vraiment pas du tout à y répondre, je vous donne les seules données que j'ai pu tirer:
$- O A$ _0 $A_1$ est rectangle en $A_1$

la somme des angles d'un triangle vaut 180° donc
d'ou l'angle en $A_0$ = (/6)
l'énonce pose $a_n$ = $0A_n$
relation trigo dans le triangle $sin(A_0$ ) = $0A_1$ / $0A_0$ )
donc $sin(A_0$ ) = $a_{1 }$ / $a_0$ )
donc $a_0$ . $sin(A_0$ ) = $a_1$
donc $a_0$ .sin(π/6) = $a_1$
Et je ne sais pas quoi faire ^^"
On voit peut etre la definition d'une suite géométrique ?
$V_{n+1}$ = $V_n$ .q
et $V$ _{n+1} $V_n$ = q ou q = sin de ...?

J'suis bloqué somebody help ! $fichier math$

Bonjour,
Inutile de considérer l'angle de sommet A0
a1 = a0. cos ( $p i$ /3) = ??
Tu ne connais pas la valeur exacte de cos ( $p i$ /3) ?

si mais ici ce nest pas cos qu'on utilise cest sinus,
cos(π/3) = 1/2 et sin(π/3) = (√3)/2

Si tu utilises le sinus, ce n'est pas celui de ∏/3 : c'est celui de ∏/6

oui pardon, donc sin(π/6) = 1/2 et ensuite ? en quoi ca m'avance ? pour la formule générale

a1 = (1/2)a0
et c'est la même chose dans tous les autres triangles :
$a_{n+1}$ = $1/2)a_n$

oui voila jme doutais mais que vaut $a_0$ , on a la raison qui vaut (1/2) et que vaut le premier terme ?

a0

--
$a</em>{n+1}$ = $1/2)a_n$ et de manière générale on a $a_n$ = $a_o$ .(1/2)^n
$a_0$ vaut 10 c'est éccrit dans l'énoncé, t'es d'accord ?

Oui.
-_- : c'est quoi ce symbole ?

ok thx, c'est un smiley

Et thx : c'est une tangente hyperbolique ?

t'es la pour me saouler ou ?

Non : mais dorénavant adresse-toi ailleurs.
So long

Bonjour dkZ,

En effet , il va falloir que tu trouves un autre forum qui accepte des sautes d'humeur.

Ici on respecte les personnes qui acceptent de passer un peu de leur temps libre ç aider ceux qui en ont besoin et qui respectent notre travail bénévole.

Oriente toi vers les sites payants !