Réflexion d'un rayon lumineux

Bonjour à tous ! J'ai cet exercice à faire , et je ne sais pas trop comment démarrer . Pouvez-vouz m'aider ? Merci d'avance !

Le miroir parabolique, frappé en M par un rayon incident, le réfléchit en un rayon symétrique par rapport à la perpendiculaire à la tangente en M à la parabole P .
La parabole est orientée de telle sorte que les rayons du Soleil arrivent tous parallèles à l'axe de la parabole.

Dans la suite, on considère que la parabole P a pour équation y= 1/4 x²

On considère que le rayon incident [RM], où M est un point de P de coordonnées (a; 1/4 a²) et R tel que le triangle FMR soit isocèle en M.
Déterminer les coordonnées du vecteur FR dans (O;i,j). (Indication : on observera que MR = MH)
En déduire que le coefficient directeur de la droite (FR) est 1/2 a .

Bonjour,
Ton énoncé est incomplet : qui est F ? qui est H ?
Si tu peux, joins une figure.

Mais bien sur , alors H de coordonnées (2,5 ; -1) et F (0 ; 1)

Oui, mais je ne sais toujours pas qui est R.
Donne l'énoncé complet.
Ou joins une figure.

R est le symétrique de H , par rapport à M

Et (RM) est parallèle à l'axe de la parabole ?
Quelle est alors l'abscisse de M ?

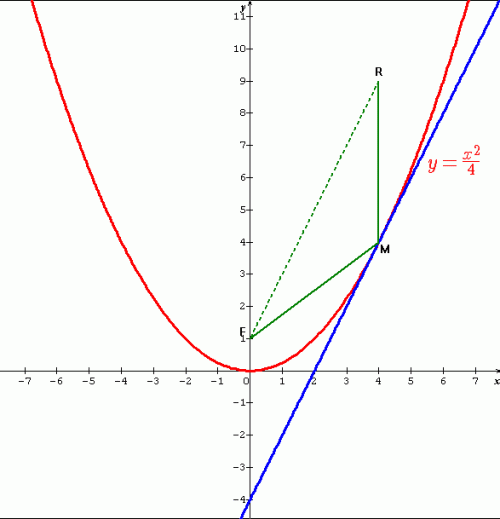$fichier math$ Voila la fonction et H est le symétrique de R par rapport a M

Place le point H.
Si (RM) est parallèle à l'axe de la parabole, quelle est l'abscisse de M ?
( tu connais celle de H ).