Aire d'un quadrilatère placé dans un rectangle

Bonjour a tous, je suis élève de 3ème et j'aurais besoin d'aide pour résoudre un problème.

Nous travaillons sur le chapitre des fonctions et j'ai un DM pour demain mais je suis perdu car je ne comprend pas ce qu'il faudrait faire car jusqu'ici on a toujours eu x|---> un calcul avec x.

Voici le problème : (désolé pour la taille de l'image)

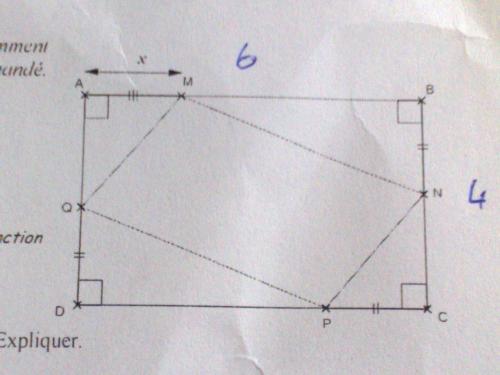
$fichier math$

ABCD est un rectangle tel que : AB = 6cm et BC = 4cm
On a placé sur les côtés de ce rectangle les points M ; N ; P et Q tels que : AM = BN = CP = DQ = x (en cm).

l'objectif de ce probleme est d'étudier l'aire du quadrilatère MNPQ en fonction de la valeur attribuée à la lettre x.

a) Quelles sont les valeurs possibles que peut prendre la lettre x ? Expliquer.

D'après ce que j'ai compris il faut faire une liste des valeurs possibles pour x mais je ne vois pas à l'aide de quoi on peut le trouver. (nous avons commencer le chapitre fonction il y a une semaine)

Merci beaucoup de votre attention.

Bonjour,

Le point M se déplace selon AB. Quelle dimension peut-on choisir pour AM ?

Inférieur a 6 non ?

Oui, donc x peut varier de 0 à 6.

J'avais pas penser de ce point de vue xD moi qui cherchait des nombres exacts pendant plus d'une heure lol

Donc si je met comme réponse : Puisque M ce trouve entre A et B, AM ne pourra pas dépasser la longueur AB donc x varie de 0 a 6.

Le prof devrai me mettre bon ?

Oui,
tu peux éventuellement préciser que si M n'est pas en A et B alors x appartient à ]0;6[.

Je te remercie.

Sinon il reste un petit truc, comme am=bn=co=dq = X donc si je met la valeur de x varie de 0 a 4 ca serait plus précis non ?

Exact, Il faut prendre en compte les deux côtés.
Donc x appartient à ]0;4[

Merci beaucoup pour ton aide

(C'est le mauvais côtés de mon prof il est sympa mais quand il nous donne des DM il le donne sans aucune explication et c'est souvent des trucs qu'on a même pas vu ou qu'on va voir après la correction.)

Une autre question super simple même stupide xD mais comme je m'y connais pas je préfère me renseigner.

Alors pour calculer l'aire d'un triangle il vaut mieux écrire base x hauteur ou longueur x largeur ? (j'ai oublier a quoi correspond la base c'est pour ça que j'hesite.)

Aire d'un triangle : base × hauteur/ 2

Tu as le cas particulier du triangle rectangle .....

quel est le cas particulier du triangle rectangle ?

Applique la formule pour le triangle AMQ.

Je pense que j'ai trouver.

Pour calculer l'aire d'un triangle il nous faut base x hauteur / 2

Base AMQ = 3
Hauteur AMQ = 4-3 = 1

3x1/2
=1.5

Tu dois faire le calcul avec AM = x.

Excuse moi mais j'ai pas compris ce que tu veux dire

Sinon je tient a préciser que j'ai changer de question et ils m'ont donner la valeur de x.

b) Dans cette question on suppose que x = 3cm
calculer l'aire des triangles suivants : AMQ ; BMN ; PNC et DQP
calculer alors l'aire du quadrilatère MNPQ.

Desolé de ne pas l'avoir dit enfin tout facon ma question au départ c'était juste de savoir si il fallait mettre base x hauteur ou largeur x longueur lol.

Comment as-tu trouvé les valeurs 3 et 1 ?

je viens de l'écrire juste au deçu de ton post enfin désolé c'est de ma faute xD j'avais écrit que la question a alors que la j'ai une grande feuille devant moi ^^

D'accord pour l'aire du triangle AMQ.

j'ai fait les autres triangles aussi de la même façon.

Et là je vais additioner l'air de chacun des triangle (1.5+1.5+4.5+4.5) et le soustraire de l'air du grand rectangle 6x4 (24-12=12)

C'est juste.

A partir de maintenant on n'attribue plus de valeur précise à la lettre x (on garde donc la lettre x pour désigner les 4 longueurs AM;BN;CP et DQ)

a) Exprimer en fonction de x l'aire de chacun des triangles suivants : AMQ ; BMN ; PNC et DQP.

Base AMQ =x
Hauteur AMQ = 4-x

Aire = x x (4-x)

Est ce correct ? ou faut il approfondir (enfin je sais même pas si on peut)

N'oublie pas de diviser par 2

Aire d'un triangle : base × hauteur /2

A oui c'est vrai et après c'est correct ?

x x (4-x) /2

Oui c'est correct.

b) A l'aide des réponses précédentes exprimer en fonction de x l'aire du quadrilatère MNPQ.

c) En développant et réduisant l'expression trouvée à la question précédente montrer que l'aire du quadrilatère MNPQ(en fonction de x) est égale à : 2x² -10x+24

J'y arrive plus xD

Tu as calculé l'aire du triangle MBN ?

oui j'ai calculer chaque triangle sa fait x x (4-x)/2 et x x (6-x)/2

Développe et simplifie ton expression.
Puis tu exprimes l'aire du quadrilatère.

j'arrive pas a le développer :rolling_eyes:

Pour la b) j'ai mis L'air du quadrilatère MNPQ est égale à x x (4-x) + x x (4-x) + x x (6-x) + x x (6-x)

et la c) je n'arrive pas

Tu as oublié le diviser par 2
C'est difficile à lire car tu mets x pour multiplier.
x(4-x) = x fois 4 - x fois x = 4x - x²

applique à
x(6-x) =

Puis additionne les deux

je dois faire le calcul que tu me montre pour la b) ou la c) ?

Je suis perdu.

Pour la question b
Aire du quadrilatère tu dois trouver
24 -x(4-x) -x(6-x)

Pour la question c tu développes en utilisant la méthode indiquée dans mon précédent post.

salut ^^

J'y suis toujours dans ce long DM (pour l'instant sa m'a prit 5 pages et j'écris petit en + ) mais c'est presque fini xD donc je voudrais savoir comment justifier que des côtés opposés d'un quadrilatère ont toujours la même longueur quelle que soit la valeur de x.

Puis l'autre question est la nature de ce quadrilatère donc je suppose que c'est un rectangle mais il faut le justifier (j'ai aucune idée de la justification)

Pour la longueur des côtés, compare les triangles.

Pourquoi un rectangle ?

non mais je pense avoir fini avec les triangles, attends j'ai pas mis assez d'info.

4eme partie

Déterminer la(les) valeur(s) de x pour laquelle(lesquelles) l'aire du quadrilatère MNPQ est égale à 13.5cm².

LA fonction f est définie par : f : x |--> 2x²-10x+24

Puis j'ai une serie de 5 questions auxquels j'ai répondu ^^

A la fin à l'aide d'un graphique j'ai trouver que x= 3.5 pile et un autre nombre aux alentour de 1.6

5eme partie
Lire sur le graphique la valeur de x pour laquelle la valeur de l'aire du quadrilatère MNPQ semble minimal
C'est 11.5²

b)Justifier que les côtés opposés du quadrilatère MNPQ ont toujours la même longueur quelle que soit la valeur attribuée a la lettre x.
(J'y arrive pas)

c) Quelle est alors la nature du quadrilatère MNPS quelle que soit la valeur attribuée à la lettre x ? justifier.

Je propose :

Les côtés opposés du quadrilatères on la meme longueur quelque soit la valeur de x car l'air du quadrilatère reste 13.5².

Qu'en dis tu ?

Compare les triangles MBN et DQP que peut-on dire de MN et QP ?
Puis les triangles NPC et AMQ.