Problème math : Recherche d'une aire maximale

bonjour je suis élève en seconde et mon professeur de math nous a donné un problème de math vraiment difficile et je n'arrive pa à trouver la solution pouvez-vous m'aidez ? merci
Voici le problème.

Probleme:Recherche d'une aire maximale

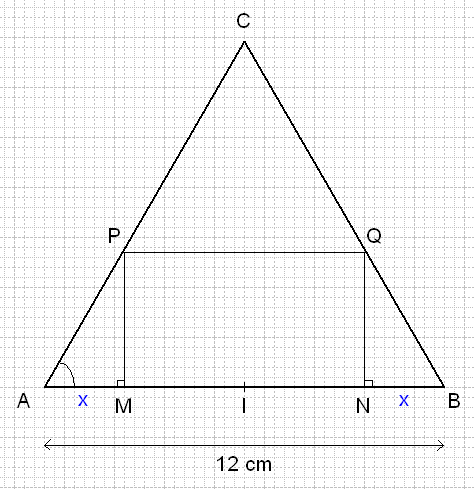
ABC est un triangle équilatéral de côté 12 cm, I est le milieu du segment (AB)
M est un point variable du segment (ab) et N est le point du segment (ab) distinct de M tel que AM=NB.
Q est le point du segment (bc) et P est le point du segment (cp) tels que MNQP soit un rectangle.
Faire une figure

Partie I: Conjecture
A L'aide du logiciel géoplan conjecturer la valeur de AM pour laquelle l'aire de rectangle MNQP est maximale et donner ce maximum .
Nous avons obtenu 3 en maximale pour la longueur AM.

Notons x la longueur AM.
Trouver l'expression de l'aire du rectangle MNQP:f(x).Donner l'ensemble de définition de f.
2)Vérifier que le maximum trouvé dans la partie I est une valeur approchée de f(3) .
3)Démontrer que f(3) est le maximum de l'aire du rectangle MNQP.
Donner les dimensions du rectangle d'aire maximale

Bonsoir lilouca,

L'aire du rectangle MNQP est égale à MN × MP. Ca, je ne pense pas que ça te pose prbl.

Exprime la longueur MN en fonction de x, connaissant AB = 12 cm.
Le triangle ABC est équilatéral. Que peux-tu dire de l'angle MAP ?
MNQP est un rectangle. Quel est la nature du triangle AMP ?
Dans ce triangle AMP particulier, tu connais une longueur AM = x et l'angle MAP.

Essaie d'exprimer la longueur MP en fonction de x ?

salut

alors avec toute cette démarche ça n'est plus un problème.

Citation

Notons x la longueur AM. Trouver l'expression f(x) de l'aire du rectangle MNQP. Donner l'ensemble de définition de f.

l'aire est donnée par MP×PQ.

facile : en fonction de x, on a PQ = ... ?

moins facile : dans AIC utilise le théorème de Thalès pour trouver MP en fonction de x

*remarque *: on a IC = 6√3 avec Pythagore par exemple.

[oups doublon : je laisse la main, NdZ]

Salut Zauctore,

Effectivement, Thales dans AIC ... c'est pas mal non plus. Marrant, quand l'énoncé ne parle pas de parallèles, on y pense pas (enfin, moi je n'y pense pas)

Lilouca nous fera peut-être les deux méthodes