Application du théorème de Thalès poussé !

ABCD est un trapèze de base [AB] et [CD].
On pose AB=a et CD=b.
M et N sont les milieux respectifs de [CB] et de [DA].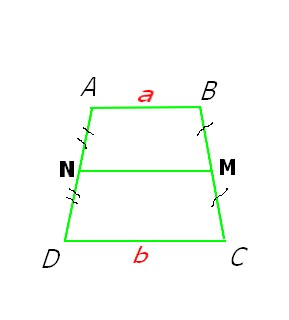

$fichier math$

Démontrer que MN=(a+b)/2

Je pense que pour cela il faudrai tracé AC

Bonjour,
Trace [BD] qui coupe [MN] en P.
Que peux-tu dire de P ?

Beh je sais pas...

Que sais-tu de la droite (MN) ?

M= milieu de [BC]
N= milieu de [AD]

Ce n'est pas ce que je te demande :
Citation
Que sais-tu de la droite (MN) ?

... Je sais pas je vois pas

Que signifie " ABCD est un trapèze" ?

Ca signifie que AB et parallère la DC

la droite (AB) est parallèle à la droite (DC).
Tu ne peux rien dire de la droite (MN) sachant que M est le milieu de [BC] et N celui de [AD] ?

Beh j'hésite a dire que MN et parallèle a AB et CD mais il faut le prouver

Tu ne l'as pas vu en classe ?
Dans ce cas il faut faire une démonstration préalable.
Oublie Net fais une nouvelle figure.
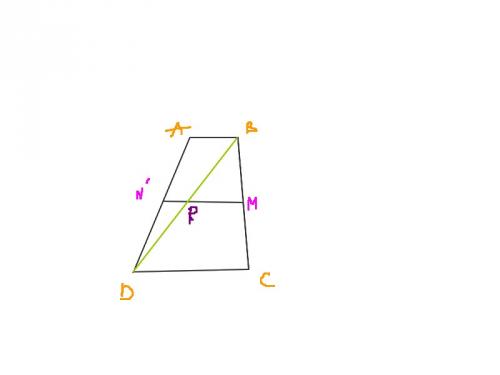
M est le milieu de [BC]. Trace la droite passant par M et parallèle à (AB) et (CD) : elle coupe [AD] en N' et [BD] en P' ( c'est exprès que je change les noms ).

Que peux-tu dire de P' ? ( utilise le triangle BCD ).

Si une droite passe par le milieu d'un côté d'un triangle et si ...

EUUUH..

$fichier math$

Oui, regarde mes deux précédents messages.

Si une droite passe par le milieu de d'un coté d'un triangle et si elle est parallèle a un un autre coté alors elle coupe le coté en son milieu

le troisième côté.
BCD est un triangle, M est le milieu de [BC], la droite (MP') est parallèle à la droite (CD), donc ... ?

Donc MP coupe BD en son milieu ?

(Mais enfète mon prof il nous a fait :
Pour trouver que MN=(a+b)/2 il faut procédé par étape.

Il faut démontrer que (MN) est parallèle à (DC)

Mais dans ce que tu me dis t'inclue que les deux droites sont forcement parallèle. On peut pas le prouver que les deux droites sont parallèle ? )

Citation
Dans ce cas il faut faire une démonstration préalable.
Oublie N et fais une nouvelle figure.
M est le milieu de [BC]. Trace la droite passant par M et parallèle à (AB) et (CD) : elle coupe [AD] en N' et [BD] en P' ( c'est exprès que je change les noms ).Je ne sais pas encore si (MN) et (CD) sont parallèles, je fais donc comme si je ne le savais pas.
J'ai dit que (MN') était parallèle à (CD) et (AB), (MN') pas (MN).Je t'ai fait refaire une autre figure afin de ne pas embrouiller la première.
Raisonne uniquement sur cette autre figure, on verra ensuite comment la relier à la première.
La conclusion du théorème sur la droite des milieux est donc que P' est le milieu de [BD], P' pas P.
Dis-moi si tu comprends.
En fait, on fait comme s'il s'agissait d'un
autreexercice.

Ok oui je comprend M et le milieu de BC
P' et le milieu de BD parce que MP' et parallèle a DC et passe par le milieu de BC dans la nouvelle figure du nouvel exercice ^^

Maintenant, toujours pour ce nouvel exercice, utilise le triangle ABD, et le même théorème.

N' est le milieu de [AD] et
NP et parallèle a AB
Donc P' et le milieu de [BD]

Non : tu raisonnes à l'envers :
On sait que P' est le milieu de [BD] ( question précédente ) et que (P'N') ( il n'y a pas ici de point P ) est parallèle à (AB) , donc ...?

N' coupe AD en son milieu

Tu t'exprimes mal : N' ne "coupe" rien : c'est un point.
N' est le milieu de [AD].
As-tu compris ce "second" exercice ?

oui

Alors on peut continuer et faire le lien avec ton exercice.
N' est le milieu de [AD], mais N est aussi le milieu de [AD], or un segment n'a qu'un seul milieu, donc N et N' sont confondus : donc la droite (MN') est la même que la droite (MN) .
(MN') a été supposée parallèle à (CD) et (AB) , donc (MN) qui est la même droite est parallèle à (CD) et (AB).
De plus, P et P' sont confondus.
Tu sais maintenant que (MN) est parallèle à (CD) et (AB), tu peux continuer l'exercice.
Dans le triangle BCD, que peux-tu dire de MP ?

MP= (DC)/2

Fais la même chose dans le triangle ABD

NP= (AB)/2

Tu y es presque. Tu dois maintenant être capable de démontrer que MN = (a+b)/2

MP=b/2
NP=a/2

b/2 + a/2 = b+a/2

Oui, mais est-ce MN ?

Mais la on a pas utiliser Thalès enfète..

Réponds d'abord à ma question.

Beh oui puisque MP+NP=MN

OK. Mais on a MN = MP + PN parce que P est situé entre M et N ( ça ne marcherait pas si le trapèze était "croisé" ).
Maintenant tu dis qu'on n'a pas utilisé Thalès "en fête" ( c'est joyeux Thalès ... ) .
Mais si : les théorèmes sur les droites des milieux dans un triangle sont en fait ( et même " en fête" ) des cas particuliers du théorème de Thalès.
Tu vois pourquoi ?

non je vois pas

(et ca par contre c'est pas très festif) ..